Producto vectorial de vectores

Se llama producto vectorial o producto cruz de vectores a y b el vector c, cuya longitud númericamente equivale al área del paralelogramo constuido en vectores a y b, perpendicular al plano de estos vectores y dirigido de tal manera que la revolución mínima del a hacia b en torno al vector c se haga de la derecha a la izquierda, si verlo del final del vector c.

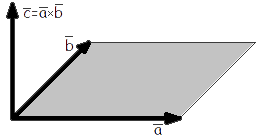fig. 1

Producto vectorial de vectores a = {a_x; a_y; a_z} y b = {b_x; b_y; b_z} ven el sistema cartesiano de coordenadas – es un vector, cuyo valor se puede calcular, utilizando las fórmulas siguientes:

a × b = ijk a_xa_ya_z b_xb_yb_z = i (a_yb_z - a_zb_y) - j (a_xb_z - a_zb_x) + k (a_xb_y - a_yb_x)

a × b = {a_yb_z - a_zb_y; a_zb_x - a_xb_z; a_xb_y - a_yb_x}

Propiedades del producto vectorial

Interpretación geométrica geométrico del producto vectorial. Módulo del producto vectorial de dos vectores a y b equivale al área del paralelogramo construído en estos vectores.
Producto vectorial de dos vectores que no son nulos a y b equivale a cero sólo cuando los vectores son colineales
Si el vector c equivale al producto vectorial de los vectores a y b, entonces es perpendicular a estos vectores.
a × b = -b × a
(k a) × b = a × (k b) = k (a × b)
(a + b) × c = a × c + b × c

Ejemplo 1. Calcular producto vectorial de los vectores a = {1; 2; 3} y b = {2; 1; -2}.

Solución

a × b =	i	j	k	=
	1	2	3
	2	1	-2

= i(2 · (-2) - 3 · 1) - j(1 · (-2) - 2 · 3) + k(1 · 1 - 2 · 2) =

= i(-4 - 3) - j(-2 - 6) + k(1 - 4) = -7i + 8j - 3k = {-7; 8; -3}

Online calculadora. Producto vectorial de vectores

Ejercicios del tema producto vectorial de vectores

Vectores Calculación del vector dado en las coordenadas cartesianas de sus puntos inicial y final Módulo del vector. Longitud del vector Cosenos directores de un vector Igualdad de vectores Vectores ortogonales Vectores colineales Vectores coplanares Ángulo entre vectores Proyección de un vector Suma y diferencia de dos vectores Multiplicación del vector por un número Producto escalar de vectores Producto vectorial de vectores Producto mixto Descomposición del vector en una base

Online calculadoras con vectores

Ecuaciones y problemas con vectores en plano

Ecuaciones y problemas con vectores en espacio

Dejar comentario