Descomposición del vector en una base

Combinación lineal de vectores a₁, ..., a_n con coeficientes x₁, ..., x_n se llama el vector

x₁a₁ + ... + x_na_n.

Para descomponer el vector b en vectores básicos a₁, ..., a_n, hace falta calcular coeficientes x₁, ..., x_n, a los cuáles la combinación lineal de vectores a₁, ..., a_n equivale al vector b:

con esto los coeficientes x₁, ..., x_n, se llaman las coordenadas del vector b en base a₁, ..., a_n.

Ejemplo. Descomponer el vector b = {8; 1} en vectores básicos p = {1; 2} y q = {3; 1}.

Solución:

Hacemos una ecuación vectorial

xp + yq = b,

la cual se puede presentar en forma del sistema de ecuaciones lineales

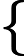	1x + 3y = 8
	2x + 1y = 1

De la primera ecuación sacamos x

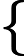	x = 8 - 3y
	2x + y = 1

Coloquemos x en la segunda ecuación.

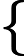	x = 8 - 3y
	2(8 - 3y) + y = 1

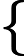	x = 8 - 3y
	16 - 6y + y = 1

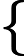	x = 8 - 3y
	5y = 15

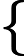	x = 8 - 3y
	y = 3

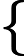	x = 8 - 3·3
	y = 3

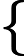	x = -1
	y = 3

Resultado: b = -p + 3q.