Ángulo entre la recta y el plano
Fórmula para hallar el ángulo entre la recta y el plano
Si en el plano tenemos dados el vector director de la recta L
s = {l; m; n}
y la ecuación del plano
Ax + By + Cz + D = 0,
entonces el ángulo entre esta recta y el plano se puede hallar aplicando la fórmula
| sin φ = | | A · l + B · m + C · n | |
| √A2 + B2 + C2 · √l2 + m2 + n2 |
Deducción de la fórmula para hallar el ángulo entre la recta y el plano
Desde la ecuación de la recta se puede hallar el vector director de la recta
s = {l; m; n}Desde la ecuación del plano el vector normal al plano tiene el aspecto siguiente
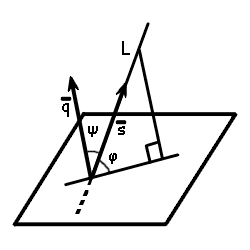
q = {A; B; C}Desde las fórmulas del producto escalar de vectores vamos a hallar el coseno del ángulo entre el normal al plano y el vector director de la recta
| cos ψ = | | q · s | |
| | s | · |q | |
Ya que φ = 90° - ψ, entonces el seno del ángulo entre la recta y el plano es sin φ = cos ψ.
Expresando el producto escalar de vectores y el módulo de vectores por medio de sus coordenadas vamos a obtener una fórmula para hallar el ángulo entre la recta y el plano.
Ejemplo de como hallar el ángulo entre la recta y el plano
Ejemplo 1. Hallar el ángulo entre la recta
x - 4
=
y + 2
= -
z - 6
2
6
3
y el plano x - 2y + 3z + 4 = 0.
Solución.
Desde la ecuación de la recta vamos a hallar el vector director
s = {2; 6; -3}
Desde la ecuación del plano vamos a hallar el vector normal al plano
q = {1; -2; 3}
Utilizando la fórmula vamos a hallar el ángulo entre la recta y el plano
sin φ =
| 2 · 1 + 6 · (-2) + (-3) · 3 |
=
√22 + 62 + (-3)2 · √12 + (-2)2 + 32
sin φ =
| 2 - 12 - 9 |
=
19
=
19
√4 + 36 + 9 · √1 + 4 + 9
√49 · √14
7√14
Resultado:
sin φ =
19
7√14
| x - 4 | = | y + 2 | = - | z - 6 |
| 2 | 6 | 3 |
Solución.
Desde la ecuación de la recta vamos a hallar el vector director
s = {2; 6; -3}Desde la ecuación del plano vamos a hallar el vector normal al plano
q = {1; -2; 3}Utilizando la fórmula vamos a hallar el ángulo entre la recta y el plano
| sin φ = | | 2 · 1 + 6 · (-2) + (-3) · 3 | | = |
| √22 + 62 + (-3)2 · √12 + (-2)2 + 32 |
| sin φ = | | 2 - 12 - 9 | | = | 19 | = | 19 |
| √4 + 36 + 9 · √1 + 4 + 9 | √49 · √14 | 7√14 |
| Resultado: |
|
Dejar comentario
