Trapecio isósceles. Fórmulas, características y propiedades del trapecio isósceles

Navegación por la página: Definición del trapecio isósceles Características del trapecio isósceles Propiedades básicas del trapecio isósceles Lados del trapecio isósceles Mediana del trapecio isósceles Altura del trapecio isósceles Diagonales del trapecio isósceles Área del trapecio isósceles Circunferencia circunscrita alrededor del trapecio

Fórmulas y propiedades del trapecio

Definición.

Un trapecio isósceles es aquel cuyos lados laterales son iguales.

En esta página están presentadas las fórmulas típicas para el trapecio isósceles. No olvide que para un trapecio isósceles son vigentes todas las fórmulas y propiedades del trapecio.

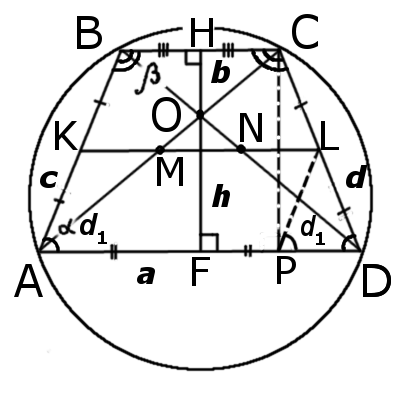Imagen del trapecio isósceles con signos

fig.1

Características del trapecio isósceles

Es isósceles un trapecio si se cumple una de estas condiciones:

1. los ángulos al lado de la base son iguales:

∠ABC = ∠BCD и ∠BAD = ∠ADC

2. las diagonales son iguales:

AC = BD

3. los ángulos son iguales entre las diagonales y las bases:

∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

4. la suma de los ángulos opuestos equivale a 180°:

∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

5. alrededor del trapecio se puede circunscribir un círculo

Propiedades básicas del trapecio isósceles

1. La suma de los ángulos adyacentes al lado lateral de un trapecio isósceles equivale a 180°:

∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°

2. Si se puede inscribir una circunferencia en el trapecio isósceles entonces el lado lateral equivale a la mediana del trapecio:

AB = CD = m

3. Alrededor del trapecio isósceles se puede circunscribir una circunferencia

4. Si las diagonales son perpendiculares entre si entonces la altura equivale a la semisuma de las bases (mediana):

h = m

5. Si las diagonales son perpendiculares entre si entonces el área del trapecio equivale al cuadrado de la altura:

A_ABCD = h²

6. Si se puede inscribir una circunferencia en el trapecio isósceles entonces el cuadrado de la altura equivale al producto de las bases del trapecio:

h² = BC · AD

7. Suma de los cuadrados de las diagonales equivale a la suma de los cuadrados de los lados laterales más el producto doble de las bases del trapecio:

AC² + BD² = AB² + CD² + 2BC · AD

8. La recta que atraviesa los centros de las bases es perpendicular a las bases y es el eje de simetría del trapecio:

HF ┴ BC, HF ┴ AD

9. La altura (CP) bajada del vértice (C) sobre la base mayor (AD) la divide en el segmento mayor (AP) que equivale a la semisuma de las bases y en el segmento menor (PD) que equivale a la semiresta de las bases:

AP =	BC + AD
	2

PD =	AD - BC
	2

10. Véase también las propiedades del trapecio

Lados del trapecio isósceles

Fórmulas de las longitudes de los lados del trapecio isósceles:

1. Fórmulas de la longitud de los lados a través de otros lados, la altura y un ángulo:

a = b + 2h ctg α = b + 2c cos α

b = a - 2h ctg α = a - 2c cos α

c =	h	=	a - b
	sin α		2 cos α

2. Fórmula de la longitud de los lados del trapecio a través de las diagonales y otros lados:

a =	d₁² - c²	b =	d₁² - c²	c = √d₁² - ab
	b		a

3. Fórmulas de la longitud de las bases a través del área, la altura y otra base:

a =	2A	- b b =	2A	- a
	h		h

4. Fórmulas de la longitud del lado lateral a través del área, la mediana y el ángulo al lado de la base:

с =	A
	m sin α

5. Fórmulas de la longitud del lado lateral a través del área, la base y el ángulo al lado de la base:

с =	2A
	(a + b) sin α

Mediana del trapecio isósceles

Fórmulas de la longitud de la mediana del trapecio isósceles:

1. Fórmula para hallar la longitud de la mediana a través de la base, la altura y el ángulo al lado de la base:

m = a - h ctg α = b + h ctg α = a - √c² - h² = b + √c² - h²

2. Fórmula de la mediana del trapecio a través del área y un lado:

m =	A
	c sin α

Altura del trapecio isósceles

Fórmulas de la longitud de la altura del trapecio isósceles:

1. Fórmula de la altura a través de los lados:

h =	1	√4c² - (a - b)²
	2

2. Fórmula de a altura a través de los lados y el ángulo adyacente a la base:

h =	a - b	tg β	= c sin β
	2

Diagonales del trapecio isósceles

Las diagonales del trapecio isósceles equivalen:

d₁ = d₂

Fórmulas de la longitud de las diagonales del trapecio isósceles:

1. Fórmula de la longitud de la diagonal a través de los lados:

d₁ = √с² + ab

2. Fórmulas de la longitud de la diagonal por el teorema de cosenos:

d₁ = √a² + c² - 2ac cos α

d₁ = √b² + c² - 2bc cos β

3. Fórmula de la longitud a través de la altura y la mediana:

d₁ = √h² + m²

4. Fórmula de la longitud a través de la altura y las bases:

d₁ =	1	√4h² + (a + b)²
	2

Área del trapecio isósceles

Fórmulas del área del trapecio isósceles:

1. Fórmula del área a través de los lados:

A =	a + b	√4c² - (a - b)²
	4

2. Fórmula del área a través de los lados y un ángulo:

A = (b + c cos α) c sin α = (a - c cos α) c sin α

3. Fórmula del área a través del radio de la circunferencia inscrita y el ángulo entre la base y el lado lateral:

A =	4 r ²	=	4 r ²
	sin α		sin β

4. Fórmula del área a través de las bases y el ángulo entre la base y el lado lateral:

A =	ab	=	ab
	sin α		sin β

5. Fórmula del área del trapecio isósceles en el cual se puede inscribir una circunferencia:

A = (a + b) · r = √ab·c = √ab·m

6. Fórmula del área a través de las diagonales y el ángulo entre ellas:

A =	d₁²	· sin γ	=	d₁²	· sin δ
	2			2

7. Fórmula del área a través de la mediana, un lado lateral y el ángulo al lado de la base:

A = mc sin α = mc sin β

8. Fórmula del área a través de la base y la altura:

A =	a + b	· h
	2

Circunferencia circunscrita alrededor del trapecio

¡¡¡Se puede sólo circunscribir una circunferencia alrededor de un trapecio isósceles!!!

Fórmula para hallar el radio de la circunferencia circunscrita alrededor de un trapecio:

1. Fórmula del radio a través de los lados y una diagonal:

R =	a·c·d₁
	4√p(p - a)(p - c)(p - d₁)

donde

p =	a + c + d₁
	2

a - la base mayor

Fórmulas geométricas Triángulo. Fórmulas y propiedades de triángulos Cuadrado. Fórmulas y propiedades de un cuadrado Rectángulo. Fórmulas y propiedades de un rectángulo Paralelogramo. Fórmulas y propiedades de un paralelogramo Rombo. Fórmulas y propiedades de un rombo Trapecio. Fórmulas y propiedades de un trapecio - Trapecio isósceles. Fórmulas y propiedades de un trapecio isósceles - Trapecio rectángulo. Fórmulas y propiedades de un trapecio rectángulo Polígono regular. Fórmulas, características y propiedades del polígono regular Circunferencia, círculo, segmento circular, sector circular. Fórmulas y propiedades Elipse. Fórmulas, atributos y propiedades de la elipse Fórmulas del área de las figuras geométricas Fórmulas del perimetro de las figuras geométricas Fórmulas del volumen de las figuras geométricas Fórmulas de área superficial de figuras geométricas

Todas tablas y fórmulas

Dejar comentario