Elipse. Fórmulas, atributos y propiedades de la elipse

Navegación por la página: Definición de la elipse Elementos de la elipse Propiedades básicas de la elipse Ecuación de la elipse Radio del círculo inscrito en la elipse Radio del círculo circunscrito a la elipse Área de la elipse Área de un segmento de la elipse Fórmula del perímetro de la elipse por aproximación Longitud de un arco de la elipse

Definición de la elipse

Definición.

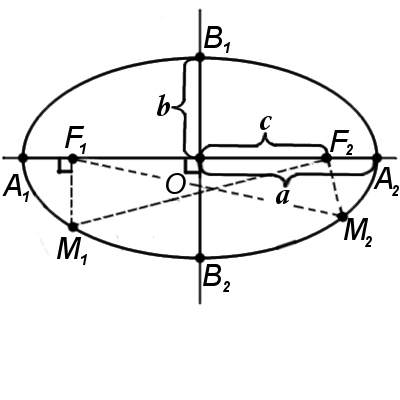
La elipse es la curva plana y cerrada, cuya suma de distancias desde cada punto hacia dos puntos F₁ y F₂ es constante. Los puntos F₁ y F₂ se denominanan los focos de la elipse.

F₁M₁ + F₂M₁ = F₁M₂ + F₂M₂ = A₁A₂ = const


Рис.1		Рис.2

Elementos de la elipse

F₁ y F₂ - focos de la elipse

Ejes de la elipse.

А₁А₂ = 2a - eje mayor de la elipse (pasa por los focos de la elipse)

B₁B₂ = 2b - eje menor de la elipse (es perpendicular al eje mayor de la elipse y pasa por su centro)

a - el semieje mayor de la elipse

b - el semieje menor de la elipse

O - centro de la elipse (el punto de intersección de los ejes mayor y menor de la elipse)

Los vértices de la elipse A₁, A₂, B₁, B₂ son puntos de intersección de la elipse con los ejes menor y mayor de la elipse.

El diámetro de la elipse es un segmento que une dos puntos de la elipse pasando por su centro.

La distancia focal c es una mitad del segmento que une los focos de la elipse.

La excentricidad de la elipse e caracteriza su extensión y se determina por la razón entre su distancia focal c y su semieje mayor a. Para una elipse la excentricidad siempre es 0 < e < 1, para un círculo e = 0, para una parábola e = 1, para una hipérbola e > 1.

e =	c
	a

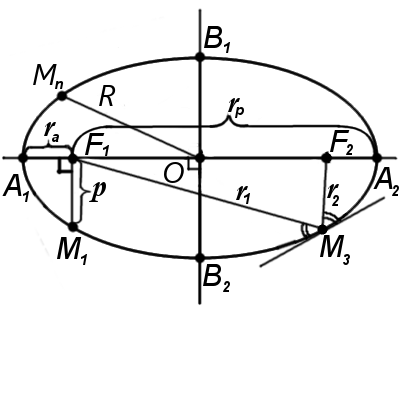
Los radios focales de la elipse r₁, r₂ son la distancia de un punto en la elipse hacia sus focos.

El radio de la elipse R es el segmento que une el centro de la elipse O con un punto en esta elipse.

R =	ab	=	b
	√a²sin²φ + b²cos²φ		√1 - e²cos²φ

donde e - e es la excentricidad de la elipse, φ - es el ángulo entre el radio y el eje mayor A₁A₂.

El perímetro focal de la elipse p es el segmento que sale del foco de la elipse y es perpendicular al semieje mayor:

p =	b²
	a

El achatamiento (o elipticidad) k es la razón de la longitud del semieje menor al semieje mayor. Ya que el semieje menor es siempre más corto que el semieje mayor, entonces k < 1, para el círculo k = 1:

k =	b
	a

k = √1 - e²

donde e es la excentricidad.

El achatamiento de la elipse (1 - k) es la medida que equivale a la diferencia entre 1 y elipticidad:

1 - k =	a - b
	a

Las directrices de la elipse son dos rectas perpendiculares al eje focal de la elipse que la cruzan por la distancia ae del centro de la elipse. La distancia desde el foco a la directriz es pe.

Propiedades básicas de la elipse

1. El ángulo entre la recta tangente de elipse y el radio focal r₁ es igual al ángulo entre la recta tangente y el radio focal r₂ (Imagen 2, punto M₃).

2. La ecuación de la recta tangente de la elipse en punto М con coordenadas (x_M, y_M):

1 =	xx_M	+	yy_M
	a²		b²

3. Si una elipse es cruzada por dos rectas paralelas, entonces el segmento que une los centros de los segmentos que resultan al cruzar las rectas y la elipse siempre pasará por el centro de la elipse. (Esta característica le deja contruir el centro de la elipse con ayuda de una regla y un compás.)

4. La evoluta de la elipse es el asteroide extendido a lo largo del eje menor.

5. Si inscribir una elipse con focos F₁ y F₂ en un triángulo ∆ ABC, entonces se cumplirá la razón:

1 =	F₁A ∙ F₂A	+	F₁B ∙ F₂B	+	F₁C ∙ F₂C
	CA ∙ AB		AB ∙ BC		BC ∙ CA

Ecuación de la elipse

Ecuación canónica de la elipse:

Esta ecuación describe una elipse en coordenadas cartesianas. Si el centro de la elipse О está al principio del sistema de coordenadas y ej eje mayor está en abscisa, entonces la elipse se describe con la siguiente ecuación:

1 =	x²	+	y²
	a²		b²

Si el centro de la elipse О está desplazado al punto con coordenadas (x_o, y_o), entonces la ecuación es:

1 =	(x - x_o)²	+	(y - y_o)²
	a²		b²

Ecuación paramétrica de la elipse:

{	x = a cos α	де 0 ≤ α < 2π
	y = b sin α

Radio del círculo inscrito en la elipse

El círculo inscrito en la elipse toca sólo dos vértices de la elipse B₁ y B₂. Por tanto el radio del círculo inscrito r será igual a la longitud del semieje menor de la elipse OB₁:
r = b

Radio del círculo circunscrito a la elipse

El círculo circunscrito a la elipse toca sólo dos vértices de la elipse A₁ y A₂. Por tanto el radio del círculo circunscrito R será igual a la longitud del semieje mayor de la elipse OA₁:
R = a

Área de la elipse

Fórmula del área de la elipse:
A = πab

Área de un segmento de la elipse

Fórmula del área de un segmento que está a la izquierda de la cuerda con coordenadas (x, y) y (x, -y):

A =	πab	-	b	(	x	√	a² - x² + a² ∙ arcsin	x	)
	2		a					a

Perímetro de la elipse

Hallar una fórmula exacta del perímetro de la elipse L es muy difícil. Abajo está una fórmula del perímetro aproximado. El error experimental máximo de esta fórmula ~0,63 %:

L ≈ 4	πab + (a - b)²
	a + b

Longitud de un arco de la elipse

Fórmulas del arco de la elipse:

1. Fórmula paramétrica para calcular un arco de la elipse por el semieje mayor a y el semieje menor b:

	t₂
l =	∫	√a²sin²t + b²cos²t dt
	t₁

2. Fórmula paramétrica para calcular un arco de la elipse por el semieje mayor a y la excentricidad e:

	t₂
l =	∫	√1 - e²cos²t dt, e < 1
	t₁

Fórmulas geométricas Triángulo. Fórmulas y propiedades de triángulos Cuadrado. Fórmulas y propiedades de un cuadrado Rectángulo. Fórmulas y propiedades de un rectángulo Paralelogramo. Fórmulas y propiedades de un paralelogramo Rombo. Fórmulas y propiedades de un rombo Trapecio. Fórmulas y propiedades de un trapecio - Trapecio isósceles. Fórmulas y propiedades de un trapecio isósceles - Trapecio rectángulo. Fórmulas y propiedades de un trapecio rectángulo Polígono regular. Fórmulas, características y propiedades del polígono regular Circunferencia, círculo, segmento circular, sector circular. Fórmulas y propiedades Elipse. Fórmulas, atributos y propiedades de la elipse Fórmulas del área de las figuras geométricas Fórmulas del perimetro de las figuras geométricas Fórmulas del volumen de las figuras geométricas Fórmulas de área superficial de figuras geométricas

Todas tablas y fórmulas

Dejar comentario