OnlineMSchool
Aprendizaje de matemáticas online.
Estudiar matemáticas con nosotros. "¡Matemáticas – es fácil!"

Circunferencia, círculo, segmento circular, sector circular. Fórmulas y propiedades

Imágenes de la circunferencia, radio, diámentro, cuerda, arco, recta secante y recta tangente Imágenes del sector y del segmento circular Imágenes del ángulo central e inscrito en la circunferencia

Definición. La circunferencia es el conjunto de todos los puntos en el plano que están situados a la misma distancia del punto dado О que se llama el centro de la circunferencia.
Definición. La circunferencia goniométrica es aquella circunferencia cuyo radio es igual a uno.
Definición. El círculo es una parte del plano limitada por una circunferencia.
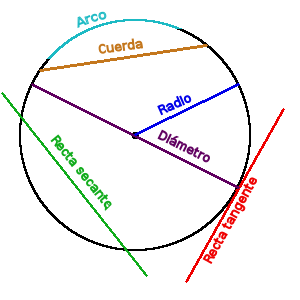
Definición. El radio de la circunferencia R es la distancia desde el centro de la circunferencia О a cualquier punto de la circunferencia.
Definición. El diámetro de la circunferencia D es el segmento que une dos puntos de la circunferencia y pasa por su centro.

Propiedades básicas de la circunferencia

1. El diámetro de la circunferencia es igual a sus dos radios.

D = 2r

2. La menor distancia desde el centro de la circunferencia a la recta secante (cuerda) es siempre menor que el radio.
3. Por tres puntos que no se sitúan en una misma recta se puede trazar sólo una circunferencia.
4. Entre todas las curvas cerradas con longitud idéntica la circunferencia tiene la mayor área.
5. Si dos circunferencia se tocan en un punto, entonces este punto está situado en la recta que atraviesa los centros de estas dos circunferencias.

Fórmulas de longitud de la circunferencia y de área del círculo

Fórmulas de longitud de la circunferencia

1. Fórmula de longitud de la circunferencia por medio del diámetro:

L = πD

2. Fórmula de longitud de la circunferencia por medio del radio:

L = 2πr

Fórmulas de área del círculo

1. Fórmula de área del círculo por medio del radio:

A = πr2

2. Fórmula de área del círculo por medio del diámetro:

A = πD24

Ecuación de la circunferencia

1. La ecuación de la circunferencia con el radio r y el centro al principio de coordenadas cartesianas:

r2 = x2 + y2

2. La ecuación de la circunferencia con el radio r y el centro en el punto con coordenadas (a, b) en coordenadas cartesianas:

r2 = (x - a)2 + (y - b)2

3. La ecuación paramétrica de la circunferencia con el radio r y el centro en el punto con coordenadas (a, b) en las coordenadas cartesianas:
{x = a + r cos t
y = b + r sin t

Recta tangente de la circunferencia y sus propiedades

Definición. La recta tangente es una recta que toca la circunferencia solamente en un punto.

Propiedades básicas de la recta tangente de la circunferencia

1. Recta tangente es siempre perpendicular al radio de la circunferencia trazado en el punto de la tangecia.
2. La menor distancia desde el centro de la circunferencia a su recta tangente es igual al radio de la circunferencia.
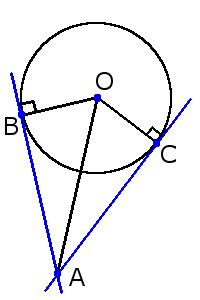
rectas tangentes
3. Si dos rectas tangentes con puntos de tocar B y C no son paralelas en una misma circunferencia, entonces se cruzan en el punto A y el segmento entre el punto de tocar y el punto de intersección en una recta tangente es igual al mismo segmento en otra recta tangente:

AB = AC

Asimismo al trazar una recta por el centro de la circunferencia O y el punto de intersección A de estas rectas tangentes, entonces los ángulos formados entre esta recta y la recta tangente serán iguales:

∠ОAС = ∠OAB

Recta secante de la circunferencia y sus propiedades

Definición. La recta secante es una recta que pasa por dos puntos de la circunferencia.

Propiedades básicas de las rectas secantes

recta secante
1. Si desde un punto fuera de la circunferencia (Q) salen dos rectas secantes que atraviesan la circunferencia en dos puntos A y B para una recta secante y C y D para otra recta secante, entonces el producto de los segmentos de estas dos rectas secantes son iguales entre si:

AQ ∙ BQ = CQ ∙ DQ

recta secante
2. Si desde un punto Q fuera de la circunferencia sale una recta secante atravesando la circunferencia en dos puntos A y B y también sale una recta tangente con el punto de tocar C, entonces el producto de los segmentos de la recta secante es igual al cuadrado de la longitud del segmento de la recta tangente:

AQ ∙ BQ = CQ2

Cuerda de la circunferencia, su longitud y propiedades

Definición. La cuerda de la circunferencia es un segmento que une dos puntos de la circunferencia.

Longitud de la cuerda

longitud de la cuerda por medio del ángulo central
1. Longitud de la cuerda por medio del ángulo central y el radio:

AB = 2r sin α2

longitud de la cuerda por medio del ángulo inscrito
2. Longitud de la cuerda por medio del ángulo inscrito y el radio:

AB = 2r sin α

Propiedades básicas de la cuerda

cuerda
1. Dos cuerdas iguales subtienden dos arcos iguales:

si las cuerdas AB = CD,

entonces los arcos ◡ AB = ◡ CD

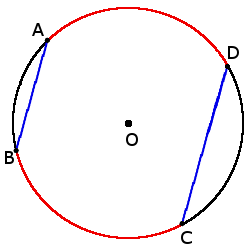
cuerda
2. Si las cuerdas son paralelas, entonces los arcos entre ellas serán iguales:

si las cuerdas AB ∣∣ CD, entonces

◡ AD = ◡ BC

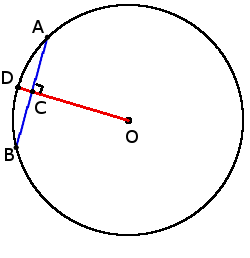
cuerda
3. Si el radio de la circunferencia es perpendicular a la cuerda, entonces él parte la cuerda por la mitad en el punto de su intersección:

si OD ┴ AB, entonces

AC = BC

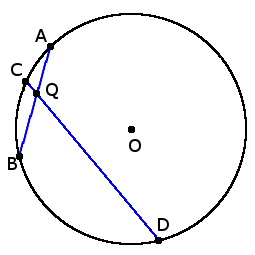
cuerda
4. Si dos cuerdas AB y CD se cruzan en el punto Q, entonces el producto de los segmentos que se han formado al cruzar una de las cuerdas es igual al producto de los segmentos de la segunda cuerda:

AQ ∙ BQ = DQ ∙ QC

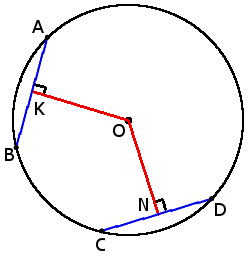
cuerda
5. Las cuerdas con la misma longitud están a la misma distancia del centro de la circunferencia:

si las cuerdas AB = CD, entonces

ON = OK

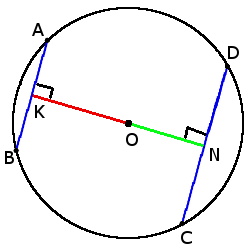
cuerda
6. Cuanto más grande sea una cuerda, más cerca ella está al centro.

si CD > AB, entonces

ON < OK

Ángulo central, ángulo inscrito en la circunferencia y sus propiedades

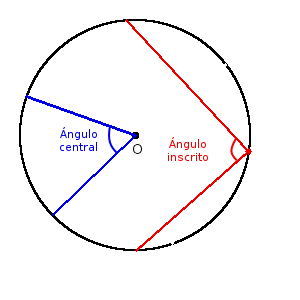
Definición. El ángulo central de la circunferencia es el ángulo cuyo vértice es el centro de la circunferencia.
Definición. El ángulo inscrito en la circunferencia es el ángulo cuyo vértice está sobre la circunferencia y los lados del ángulo atraviesan la circunferencia.

Propiedades básicas de los ángulos

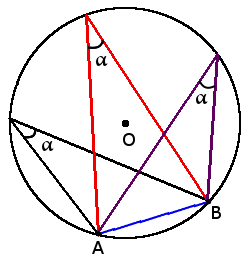
ángulos inscritos apoyados en un arco
1. Todos los ángulos inscritos, que se apoyan en un arco, son iguales.

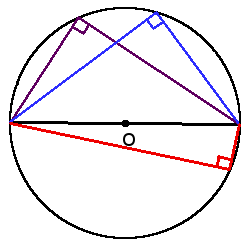
ángulo inscrito apoyado en el diámetro
2. El ángulo inscrito, que se apoya en el diámetro, será recto (90°).

ángulo inscrito y central
3. El ángulo inscrito es igual a la mitad del ángulo central que se apoya en el mismo arco

β = α2

ángulos inscritos apoyados en una cuerda
4. Si dos ángulos inscritos se apoyan en una misma cuerda y se sitúan a diferentes lados de ella, entonces la suma de estos ángulos es 180°.

α + β = 180°

Definición. El arco de la circunferencia (◡) es una parte de la circunferencia que une dos puntos en la circunferencia.
Definición. La medida de grado del arco es un ángulo entre dos radios que demarcan este arco. La medida de grado del arco es siempre igual a la medida de grado del ángulo central que demarca este arco con sus lados.
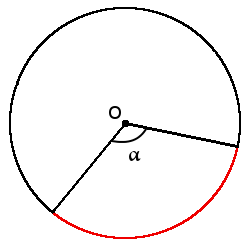
longitud del arco
Fórmula de longitud del arco por medio del ángulo central (en grados):

l = πr180°∙ α

Definición. La semicircunferencia es un arco cuyos extremos están unidos por el diámetro de la circunferencia.
Definición. El semicírculo (◓) es una parte del círculo demarcada por la semicircunferencia y el diámetro.
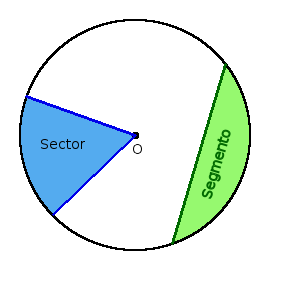
Definición. El sector (◔) es una parte del círculo demarcada por dos radios y el arco entre estos radios.
сектор
Fórmula. Fórmula de área del sector por medio del ángulo central (en grados)

A = πr2360°∙ α

Definición. El segmento es una parte del círculo demarcada por el arco y la cuerda que une sus extremos.
Definición. Las circunferencias concéntricas son las circunferencias con distintos radios que tienen un centro común.
Definición. La corona circular es una parte del plano demarcada por dos circunferencias concéntricas.
Fórmulas geométricas Triángulo. Fórmulas y propiedades de triángulos Cuadrado. Fórmulas y propiedades de un cuadrado Rectángulo. Fórmulas y propiedades de un rectángulo Paralelogramo. Fórmulas y propiedades de un paralelogramo Rombo. Fórmulas y propiedades de un rombo Trapecio. Fórmulas y propiedades de un trapecio - Trapecio isósceles. Fórmulas y propiedades de un trapecio isósceles - Trapecio rectángulo. Fórmulas y propiedades de un trapecio rectángulo Polígono regular. Fórmulas, características y propiedades del polígono regular Circunferencia, círculo, segmento circular, sector circular. Fórmulas y propiedades Elipse. Fórmulas, atributos y propiedades de la elipse Fórmulas del área de las figuras geométricas Fórmulas del perimetro de las figuras geométricas Fórmulas del volumen de las figuras geométricas Fórmulas de área superficial de figuras geométricas
Todas tablas y fórmulas

Dejar comentario

0
Follow OnlineMSchool on