Paralelogramo. Fórmulas, características y propiedades del paralelogramo

Navegación por la página: Definición del paralelogramo Características del paralelogramo Propiedades básicas del paralelogramo Lados del paralelogramo Diagonal del paralelogramo Perímetro del paralelogramo Área del paralelogramo

Definición.

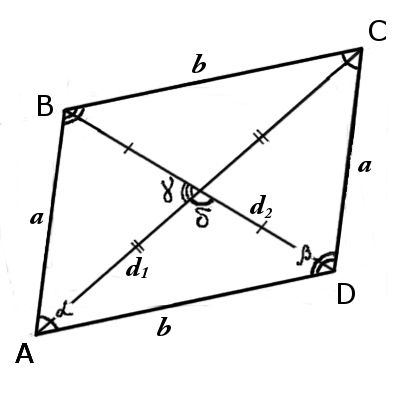
Paralelogramo es un cuadrilátero cuyos lados opuestos son paralelos a pares (se ubican en las rectas paralelas).

Los paralelogramos se diferencian tanto por el tamaño de los lados adyacentes como por los ángulos, sin embargo, los lados opuestos son iguales.


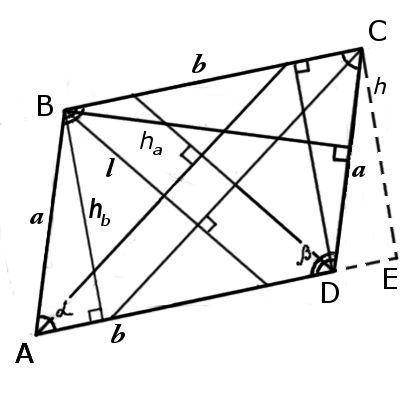
fig.1		fig.2

Características del paralelogramo

El cuadrilátero ABCD será paralelogramo si se cumple por lo menos una de las siguientes condiciones:

1. Un cuadrilátero tiene dos pares de los lados paralelos:

AB||CD, BC||AD

2. Un cuadrilátero tiene un par de los lados paralelos e iguales:

AB||CD, AB = CD (или BC||AD, BC = AD)

3. En un cuadrilátero los lados opuestos son iguales a pares:

AB = CD, BC = AD

4. En un cuadrilátero los ángulos opuestos son iguales a pares:

∠DAB = ∠BCD, ∠ABC = ∠CDA

5. En un cuadrilátero las diagonales se dividen por la mitad con el punto de intersección:

AO = OC, BO = OD

6. Suma de ángulos de cuadrilátero adyacentes a cualquier lado es 180°:

∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

7. En un cuadrilátero la suma de cuadrados de diagonales es igual a la suma de cuadrados de sus lados:

AC² + BD² = AB² + BC² + CD² + AD²

Propiedades básicas del paralelogramo

El cuadrado, el rectángulo y el rombo son paralelogramos

1. Los lados opuestos de paralelogramo tienen la longitud igual:

AB = CD, BC = AD

2. Los lados opuestos de paralelogramo son paralelos:

AB||CD, BC||AD

3. Los ángulos opuestos de paralelogramo son iguales:

∠ABC = ∠CDA, ∠BCD = ∠DAB

4. La suma de ángulos de paralelogramo es 360°:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

5. - La suma de los ángulos de paralelogramo adyacentes a cualquier lado es 180°:

∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°

6. Cada diagonal divide un paralelogramo en dos triángulos iguales

7. Dos diagonales dividen un paralelogramo en dos pares de triángualos iguales

8. Las diagonales del paralelogramo se cruzan y con el punto de su intersección se dividen por la mitad:

AO = CO =	d₁
	2
BO = DO =	d₂
	2

9. El punto de intersección de las diagonales se llama el centro de simetría de un paralelogramo

10. La suma de cuadrados de diagonales de paralelogramo es igual a la suma de cuadrados de sus lados:

AC² + BD² = 2AB² + 2BC²

11. Las bisectrices de los lados opuestos de un paralelogramo siempre son paralelas

12. Las bisectrices de los lados vecinos de un paralelogramo siempre se cruzan bajo el ángulo recto (90°)

Lados del paralelogramo

Fórmulas para hallar la longitud de los lados de un paralelogramo:

1. Fórmula para hallar los lados de un paralelogramo a través de las diagonales y el ángulo entre ellas:

a =	√d₁² + d₂² - 2d₁d₂·cosγ	=	√d₁² + d₂² + 2d₁d₂·cosδ
	2		2

b =	√d₁² + d₂² + 2d₁d₂·cosγ	=	√d₁² + d₂² - 2d₁d₂·cosδ
	2		2

2. Fórmula para hallar los lados de un paralelogramo a través de las diagonales y otro lado:

a =	√2d₁² + 2d₂² - 4b²
	2

b =	√2d₁² + 2d₂² - 4a²
	2

3. Fórmula para hallar los lados de un paralelogramo a través de la altura y el seno del ángulo:

a =	h_b
	sin α

b =	h_a
	sin α

4. Fórmula para hallar los lados de un paralelogramo a través del área y la altura:

a =	A
	h_a

b =	A
	h_b

Diagonal del paralelogramo

Definición.

Se llama la diagonal de un paralelogramo cualquier segmento que une dos vértices de los ángulos opuestos de un paralelogramo.

El paralelogramo tiene dos diagoneles – una larga d₁, y otra corta d₂

Fórmulas para hallar la longitud de las diagonales de un paralelogramo:

1. Fórmulas para hallar las diagonales de un paralelogramo a través de los lados y el coseno del ángulo β (a base del teorema de cosenos)

d₁ = √a² + b² - 2ab·cosβ

d₂ = √a² + b² + 2ab·cosβ

2. Fórmulas para hallar las diagonales de un paralelogramo a través de los lados y el coseno del ángulo α (a base del teorema de cosenos)

d₁ = √a² + b² + 2ab·cosα

d₂ = √a² + b² - 2ab·cosα

3. Fórmula para hallar las diagonales de un paralelogramo a través de dos lados y otra diagonal conocida:

d₁ = √2a² + 2b² - d₂²

d₂ = √2a² + 2b² - d₁²

4. Fórmula para hallar las diagonales de un paralelogramo a través del área, una diagonal conocida y el ángulo entre las diagonales:

d₁ =	2A	=	2A
	d₂·sinγ		d₂·sinδ

d₂ =	2A	=	2A
	d₁·sinγ		d₁·sinδ

Perímetro del paralelogramo

Definición.

Se llama el perímetro de un paralelogramo la suma de las longitudes de todos los lados de un paralelogramo.

Fórmulas para hallar la longitud de perímetro de un paralelogramo:

1. Fórmula del perímetro de un paralelogramo a través de los lados de un paralelogramo:

P = 2a + 2b = 2(a + b)

2. Fórmula del perímetro de un paralelogramo a través de un lado y dos diagonales:

P = 2a + √2d₁² + 2d₂² - 4a²

P = 2b + √2d₁² + 2d₂² - 4b²

3. - Fórmula del perímetro de un paralelogramo a través de un lado, la altura y el seno del ángulo:

P =	2(b +	h_b	)
		sin α

P =	2(a +	h_a	)
		sin α

Área del paralelogramo

Definición.

Se llama el área de un paralelogramo a un espacio limitado por los lados de un paralelogramo, o sea, dentro del perímetro de un paralelogramo.

Fórmulas para hallar el área de un paralelogramo:

1. Fórmula del área de un paralelogramo a través del lado y la altura relacionada a este lado:

A = a · h_a
A = b · h_b

2. Fórmula del área de un paralelogramo a través de dos lados y el seno del ángulo entro ellos:

A = ab sinα

A = ab sinβ

3. Fórmula del área de un paralelogramo a través de dos diagonales y el seno del ángulo entre ellas:

A =	1	d₁d₂ sin γ
	2

A =	1	d₁d₂ sin δ
	2

Fórmulas geométricas Cuadrado. Fórmulas y propiedades de un cuadrado Rectángulo. Fórmulas y propiedades de un rectángulo Paralelogramo. Fórmulas y propiedades de un paralelogramo Rombo. Fórmulas y propiedades de un rombo Trapecio. Fórmulas y propiedades de un trapecio - Trapecio isósceles. Fórmulas y propiedades de un trapecio isósceles - Trapecio rectángulo. Fórmulas y propiedades de un trapecio rectángulo Polígono regular. Fórmulas, características y propiedades del polígono regular Fórmulas del área de las figuras geométricas Fórmulas del perimetro de las figuras geométricas Fórmulas del volumen de las figuras geométricas Fórmulas de área superficial de figuras geométricas

Todas tablas y fórmulas

Dejar comentario