Ángulo entre vectores
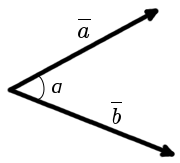
Ángulo entre dos vectores, trazados de un punto, se llama el ángulo más corto al cual hay que girar uno de los vectores alrededor de su inicio hasta la posición de co-dirección con el otro vector.
 |
El coseno del ángulo entre vectores equivale al producto escalar de dos vectores dividido en el producto de módulos de estos vectores.
Fórmula de calculación del ángulo entre vectores
| cos α = | a·b |
| |a|·|b| |
Ejemplo 1. Calcular el ángulo entre los vectores a = {3; 4} y b = {4; 3}.
Solución:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24
|a| = √32 + 42 = √9 + 16 = √25 = 5
|b| = √42 + 32 = √16 + 9 = √25 = 5
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| |a| · |b| | 5 · 5 | 25 |
Ejemplo 2. Calcular el ángulo entre los vectores a = {3; 4; 0} y b = {4; 4; 2}.
Solución:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28
|a| = √32 + 42 + 02 = √9 + 16 = √25 = 5
|b| = √42 + 42 + 22 = √16 + 16 + 4 = √36 = 6
| cos α = | a · b | = | 28 | = | 14 |
| |a| · |b| | 5 · 6 | 15 |
VectoresCalculación del vector dado en las coordenadas cartesianas de sus puntos inicial y final
Módulo del vector. Longitud del vector
Cosenos directores de un vector
Igualdad de vectores
Vectores ortogonales
Vectores colineales
Vectores coplanares
Ángulo entre vectores
Proyección de un vector
Suma y diferencia de dos vectores
Multiplicación del vector por un número
Producto escalar de vectores
Producto vectorial de vectores
Producto mixtoDescomposición del vector en una base
Dejar comentario
