Filas linealmente dependientes e independientes.
Navegación por la página:
Definición.
Se llama combinación lineal de las filas
s1,
s2, ...,
sl de la matriz A a la expresión
α1s1 + α2s2 + ... + αlsl
Definición.
Toda combinación lineal de filas es
trivial si todos sus coeficientes
αi simultáneamente son iguales a cero.
¡Nótese!
Combinación lineal trivial de las filas es igual a la
fila nula.
Definición.
Toda combinación lineal de filas es
no trivial si al menos uno de los coeficientes
αi no es igual a cero.
Definición.
Todo sistema de filas es
linealmente dependiente (LD) si existe su combinación lineal no trivial que sea igual a la fila nula.
Definición.
Todo sistema de filas es
linealmente independiente (LIN) si solo la combinación lineal trivial de filas es igual a la fila nula (no existe su combinación lineal no trivial que sea igual a la fila nula).
¡Nótese!
El sistema de filas de una
matriz cuadrada es linealmente dependiente si y sólo si el
determinante de esta matriz no es igual a cero.
¡Nótese!
El sistema de filas de una matriz cuadrada es linealmente dependiente si y sólo si el determinante de esta matriz es igual a cero.
Ejemplo 1.
Mostrar que el sistema de filas {
s1 = {2 5};
s2 = {4 10}} es linealmente dependiente.
Solución. Hagamos una combinación lineal de estas filas
α1{2 5} + α2{4 10}
Calculemos tales valores de α1, α2 que esta combinación lineal sea igual a la fila nula
α1{2 5} + α2{4 10} = {0 0}
La ecuación dada es equivalente a tal sistema de ecuaciones:
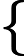 |
2α1 + 4α2 = 0 |
| 5α1 + 10α2 = 0 |
Dividamos la primera ecuación por 2 y la segunda ecuación por 5:
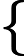 |
α1 + 2α2 = 0 |
| α1 + 2α2 = 0 |
El resultado de este sistema pueden ser números cualquieres α1 y α2 pero que: α1 = -2α2, por ejemplo, α2 = 1, α1 = -2, y eso significa que las filas s1 y s2 son linealmente dependientes.
Ejemplo 2.
Mostrar que el sistema de filas {
s1 = {2 5 1};
s2 = {4 10 0}} es linealmente independiente.
Solución. Hagamos una combinación lineal de estas filas.
α1{2 5 1} + α2{4 10 0}
Calculemos tales valores de α1, α2 esta combinación lineal sea igual a la fila nula
α1{2 5 1} + α2{4 10 0} = {0 0 0}
La ecuación dada es equivalente a tal sistema de ecuaciones:
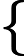 |
2α1 + 4α2 = 0 |
| 5α1 + 10α2 = 0 |
| α1 + 0α2 = 0 |
De la tercera ecuación obtenemos α1 = 0, pongamos este valor en la primera y la segunda ecuaciones:
2·0+4α2=0
5·0+10α2=0
α1=0
=>
4α2=0
10α2=0
α1=0
=>
α2 = 0
α2 = 0
α1 = 0
Ya que la combinación lineal de filas es igual a cero sólo cuando α1 = 0 y α2 = 0, entonces las filas son linealmente independientes.
