Matriz inversa

• Definición de matriz inversa
• Propiedades de matriz inversa
• Métodos del cálculo de una matriz inversa
  • Cálculo de matriz inversa por medio de matriz adjunta
  • Cálculo de matriz inversa por medio de matriz de adjuntos

Matriz inversa A⁻¹ — es una matriz cuyo producto por la matriz inicial A es igual a la matriz identidad E:

A·A^-1 = A^-1·A = E

Una matriz inversa existe sólo para las matrices cuadradas cuyo determinante no es igual a cero.

●	det(A-1) =  1 det(A)
●	(A·B)-1 = A-1·B-1
●	(A-1)T = (AT)-1
●	(kA)-1 =  A-1 k
●	(A-1)-1 = A

Si a la derecha de una matriz cuadrada escribir una matriz identidad del mismo orden y por medio de las operaciones elementales de filas transformar la matriz obtenida de tal modo que la matriz inicial se convierta en una matriz identidad, entonces la matriz resultante de la de identidad será una matriz inversa a la inicial.

Si durante la transformación en la parte izquierda de la matriz se crea una fila (columna) nula, entonces la matriz inicial no tiene matriz inversa.

Calcular matriz inversa de la matriz A

A =		2	4	1
		0	2	1
		2	1	1

Solución: Escribamos a la derecha de la matriz A una matriz identidad de orden 3:

A|E =		2	4	1	1	0	0		~
		0	2	1	0	1	0
		2	1	1	0	0	1

Transformemos la parte izquierda de la matriz obtenida en la de identidad. Para hacerlo restemos la primera fila de la tercera:

~		2	4	1	1	0	0		~
		0	2	1	0	1	0
		2 - 2	1 - 4	1 - 1	0 - 1	0 - 0	1 - 0

~		2	4	1	1	0	0		~
		0	2	1	0	1	0
		0	-3	0	-1	0	1

Dividamos la tercera fila por (-3) y la transpongamos con la segunda fila:

~		2	4	1	1	0	0		~
		0	2	1	0	1	0
		0	1	0	1/3	0	-1/3

~		2	4	1	1	0	0		~
		0	1	0	1/3	0	-1/3
		0	2	1	0	1	0

Restemos de la primera fila la segunda multiplicada por 4; de la tercera fila la segunda multiplicada por 2:

~		2 - 4·0	4 - 4·1	1 - 4·0	1 - 4·(1/3)	0 - 4·0	0 - 4·(-1/3)		~
		0	1	0	1/3	0	-1/3
		0 - 2·0	2 - 2·1	1 - 2·0	0 - 2·1/3	1 - 2·0	0 - 2·(-1/3)

~		2	0	1	-1/3	0	4/3		~
		0	1	0	1/3	0	-1/3
		0	0	1	-2/3	1	2/3

Restemos la tercera fila de la primera:

~		2 - 0	0 - 0	1 - 1	-1/3 - (-2/3)	0 - 1	4/3 - 2/3		~
		0	1	0	1/3	0	-1/3
		0	0	1	-2/3	1	2/3

~		2	0	0	1/3	-1	2/3		~
		0	1	0	1/3	0	-1/3
		0	0	1	-2/3	1	2/3

Dividamos la primera fila por 2:

~		1	0	0	1/6	-1/2	1/3
		0	1	0	1/3	0	-1/3
		0	0	1	-2/3	1	2/3

Resultado: A-1 =		1/6	-1/2	1/3
		1/3	0	-1/3
		-2/3	1	2/3

La matriz Ã, cuyos elementos son iguales a los cofactores respectivos de la matriz A es una matriz de adjuntos.

A-1 =	1	ÃT
	det(A)

Calcular matriz inversa de la matriz A

A =		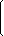2	4	1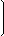
		0	2	1
		2	1	1

Solución: Calculemos el determinante de la matriz A:

det(A) =	2	4	1	=
	0	2	1
	2	1	1

= 2·2·1 + 4·1·2 + 1·0·1 - 1·2·2 - 2·1·1 - 4·0·1 = 4 + 8 + 0 - 4 - 2 - 0 = 6

Calculemos los cofactores de la matriz A:

A11 = (-1)1 + 1·	2	1	= 2·1 - 1·1 = 1
	1	1

A12 = (-1)1 + 2·	0	1	= -(0·1 - 1·2) = 2
	2	1

A13 = (-1)1 + 3·	0	2	= 0·1 - 2·2 = -4
	2	1

A21 = (-1)2 + 1·	4	1	= -(4·1 - 1·1) = -3
	1	1

A22 = (-1)2 + 2·	2	1	= 2·1 - 1·2 = 0
	2	1

A23 = (-1)2 + 3·	2	4	= -(2·1 - 4·2) = 6
	2	1

A31 = (-1)3 + 1·	4	1	= 4·1 - 1·2 = 2
	2	1

A32 = (-1)3 + 2·	2	1	= -(2·1 - 1·0) = -2
	0	1

A33 = (-1)3 + 3·	2	4	= 2·2 - 4·0 = 4
	0	2

Escribamos una matriz de adjuntos:

à =		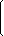1	2	-4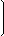
		-3	0	6
		2	-2	4

Calculemos una matriz inversa:

A-1 =  1 ÃT  =  1 det(A) 6

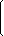1 -3 2 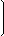2 0 -2 -4 6 4

=

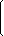1/6 -1/2 1/3 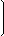1/3 0 -1/3 -2/3 1 2/3

Resultado: A-1 =		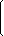1/6	-1/2	1/3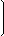
		1/3	0	-1/3
		-2/3	1	2/3