Determinante de una matriz

Navegación por la página:

Definición del determinante de una matriz
Propiedades del determinante de una matriz
Métodos del cálculo del determinante de una matriz

Determinante de una matriz es una de las principales características numéricas de una matriz cuadrada que se aplica para resolver muchos problemas.

Definición.

El determinante de la matriz n×n será el número:

det(A) =	Σ	(-1)^{N(α₁,α₂,...,α_n)}·a_α₁1·a_α₂2·...·a_{α_nn}
	(α₁,α₂,...,α_n)

donde (α₁,α₂,...,α_n) - transposición de números desde 1 a n, N(α₁,α₂,...,α_n) - número de inversiones en la transposición, el proceso de sumar se realiza en todas las transposiciones posibles del orden n.

Обозначение

Определитель матрици A обычно обозначается det(A), |A|, или ∆(A).

Propiedades del determinante de una matriz

Determinante de una matriz identidad es igual a uno:
det(E) = 1
Determinante de una matriz con dos filas (columnas) iguales es igual a cero.
Determinante de una matriz con dos filas (columnas) proporcionales es igual a cero.
Determinante de una matriz que contiene una fila (columna) nula es igual a cero.
Determinante de una matriz es igual a cero si dos (o varias) filas (columnas) de la matriz son linealmente dependientes.
Durante la transposición el valor del determinante de una matriz no se cambia:
det(A) = det(A^T)
Determinante de una matriz inversa:
det(A^-1) = det(A)^-1
Determinante de una matriz no se cambiará si a alguna de sus filas (columnas) sumar otra fila (columna) multiplicada por un cierto número.
Determinante de una matriz no se cambiará si a alguna de sus filas (columnas) sumar una combinación lineal de otras filas (columnas).
Si cambiar de posición dos filas (columnas) de una matriz, entonces el determinante de la matriz cambiará su signo.
Se puede transponer el factor común en una fila (columna) fuera del signo del determinante:
a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... k·a_i1k·a_i2...k·a_in .... a_n1a_n2...a_nn = k· a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... a_i1a_i2...a_in .... a_n1a_n2...a_nn
Si una matriz cuadrada de orden n se multiplica por un cierto número no nulo, entonce el determinante de la matriz obtenida es igual al producto del determinante de la matriz inicial por este número elevado a n:
B = k·A => det(B) = kⁿ·det(A)
donde A matriz n×n, k - número.
Si cada elemento en alguna fila del determinante es igual a la suma de dos sumandos, entonces el determinante inicial es igual a la suma de dos determinantes en los que en vez de esta fila se sitúan el primer y el segundo sumando respectivamente y las demás filas coinciden con el determinante inicial:

a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... b_i1 + c_i1b_i2 + c_i2...b_in + c_in .... a_n1a_n2...a_nn = a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... b_i1b_i2...b_in .... a_n1a_n2...a_nn + a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... c_i1c_i2...c_in .... a_n1a_n2...a_nn
Determinante de la matriz triangular superior (inferior) es igual al producto de sus elementos diagonales.
Determinante del producto de matrices es igual al producto de determinantes de estas matrices:
det(A·B) = det(A)·det(B)

Métodos del cálculo del determinante de una matriz

Cálculo del determinante de la matriz 1×1

Regla:

Para una matriz del orden 1 el valor del determinante es igual al valor de un elemento de esta matriz:

∆ = |a₁₁| = a₁₁

Cálculo del determinante de la matriz 2×2

Regla:

Para la matriz 2×2 el valor del determinante es igual a la diferencia de los productos de los elementos de la diagonal principal y secundaria:

∆ =

a₁₁	a₁₂
a₂₁	a₂₂

= a₁₁·a₂₂ - a₁₂·a₂₁

Ejemplo 1.

Calcular el determinante de la matriz A

A =

	5	7
	-4	1

Solución:

det(A) =

5	7
-4	1

= 5·1 - 7·(-4) = 5 + 28 = 33

Cálculo del determinante de la matriz 3×3

Regla del triángulo para calcular el determinante de matriz del orden 3

Regla:

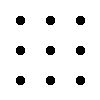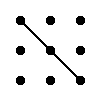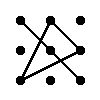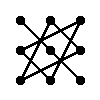Para la matriz 3×3 el valor del determinante es igual a la suma de los productos de los elementos de la diagonal principal y los productos de los elementos situados sobre los triángulos con la cara paralela a la diagonal principal de la que se sustrae el producto de los elementos de la diagonal secundaria y el producto de los elementos situados en los triángulos con la cara paralela a la diagonal secundaria.


+		–

∆ =

a₁₁	a₁₂	a₁₃
a₂₁	a₂₂	a₂₃
a₃₁	a₃₂	a₃₃

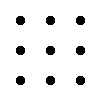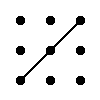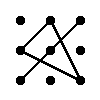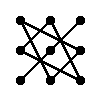= a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ - a₁₃·a₂₂·a₃₁ - a₁₁·a₂₃·a₃₂ - a₁₂·a₂₁·a₃₃

Regla de Sarrus para calcular el determinante de la matriz de orden 3.

Regla:

A la derecha del determinante se apuntan dos primeras columnas y los productos de los elementos en la diagonal principal y en las diagonales paralelas a ella, se aplican con el signo “más”; y los productos de los elementos de la diagonal secundaria y las diagonales paralelas a ella, se aplican con el signo “menos”:

∆ =

a₁₁	a₁₂	a₁₃	a₁₁	a₁₂
a₂₁	a₂₂	a₂₃	a₂₁	a₂₂
a₃₁	a₃₂	a₃₃	a₃₁	a₃₂

= a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ - a₁₃·a₂₂·a₃₁ - a₁₁·a₂₃·a₃₂ - a₁₂·a₂₁·a₃₃

Ejemplo 2.

Calcular el determinante de la matriz A = 571 -410 203

Solución:

det(A) = 571 -410 203 = 5·1·3 + 7·0·2 + 1·(-4)·0 - 1·1·2 - 5·0·0 - 7·(-4)·3 = 15 + 0 + 0 - 2 - 0 + 84 = 97

Cálculo del determinante de una matriz de la dimensión opcional

Desarrollo de un determinante por una fila o una columna

Regla:

Determinante de una matriz es igual a la suma de los productos de los elementos de la fila del determinante por sus cofactores:

	n
det(A) =	Σ	a_ij·A_ij	- desarrollo por la fila i
	j = 1

Regla:

Determinante de una matriz es igual a la suma de los productos de los elementos de la columna del determinante por sus cofactores:

	n
det(A) =	Σ	a_ij·A_ij	- desarrollo por la columna j
	i = 1

Cuando se desarrolla el determinante de una matriz normalmente se escoge aquella fila/columna que tenga el máximo número de los elementos nulos.

Ejemplo 3.

Calcular el determinante de la matriz A

A =

2	4	1
0	2	1
2	1	1

Solución: Calculemos el determinante de una matriz desarrollándolo por la primera columna:

det(A) =

2	4	1
0	2	1
2	1	1

= 2·(-1)¹⁺¹· 21 11 + 0·(-1)²⁺¹· 41 11 + 2·(-1)³⁺¹· 41 21 =

= 2·(2·1 - 1·1) + 2·(4·1 - 2·1) = 2·(2 - 1) + 2·(4 - 2) = 2·1 + 2·2 = 2 + 4 = 6

Ejemplo 4.

Calcular el determinante de la matriz A

A = 2411 0200 2113 4023

Solución: Calculemos el determinante de una matriz desarrollándolo por la segunda fila (tiene el mayor número de ceros):

det(A) = 2411 0200 2113 4023 = - 0· 411 113 023 + 2· 211 213 423 - 0· 241 213 403 + 0· 241 211 402 =

= 2·(2·1·3 + 1·3·4 + 1·2·2 - 1·1·4 - 2·3·2 - 1·2·3) = 2·(6 +12 + 4 - 4 - 12 - 6) = 2·0 = 0

Reducción del determinante a la forma triangular

Regla:

Utilizando las propiedades del determinante para las operaciones elementales sobre filas columnas (8 - 11,), un determinante se toma un aspecto triangular y entonces su valor será igual al producto de los elementos situados en la diagonal principal.

Ejemplo 5.

Calcular el determinante de la matriz A por medio de su reducción a la forma triangular

A = 2411 0210 2113 4023

Solución:

det(A) = 2411 0210 2113 4023

Primero obtengamos unos ceros en la primera columna debajo de la diagonal principal. Para ello sustraigamos la primera fila de la tercera, y la primera multiplicada por 2 de la cuarta fila:

det(A) = 2411 0210 2 - 21 - 41 - 13 - 1 4 - 2·20 - 4·22 - 1·23 - 1·2 = 2411 0210 0-302 0-801

Obtengamos unos ceros en la segunda columna debajo de la diagonal principal. Para ello transpongamos la segunda y la tercera columna (asimismo el determinante cambiará su signo por el contrario):

det(A) = - 2141 0120 00-32 00-81

Obtengamos unos ceros en la tercera columna debajo de la diagonal principal. Para ello sumemos a la tercera columna la cuarta multiplicada por ocho:

det(A) = - 214 + 1·81 012 + 0·80 00-3 + 2·82 00-8 + 1·81 = - 21121 0120 00132 0001 = -2·1·13·1 = -26

Teorema de Laplace

Teorema:

Digamos que ∆ - es un determinante del orden n. Escojamos en ello cualquier k filas (columnas), pero que k < n. Entonces la suma de los productos de todos los menores del orden k, contenidos en las filas (columnas) elegidas, por sus cofactores es igual al determinante.

Online calculadoras gratis para resolver problemas matemáticos con matrices

Ejercicios con matrices

Matrices. Introducción e índice Matrices: definición y términos básicos Reducción de sistema de ecuaciones lineales a matriz Tipos de matrices Multiplicación de una matriz por un número Suma y resta de matrices Multiplicación de matrices Matriz transpuesta Operaciones elementales de matrices Determinante de una matriz Menor y cofactores de una matriz Matriz inversa Filas linealmente dependientes e independientes Rango de una matriz

Dejar comentario