Proyección de un vector sobre un eje. Proyección de un vector sobre otro.
Navegación por la página:
Definición. La proyección del vector AB sobre el eje l se denomina el número que es igual al valor del segmento A1B1 del eje l, donde los puntos A1 y B1 son proyecciones de los puntos A y B sobre el eje l. (imagen. 1).
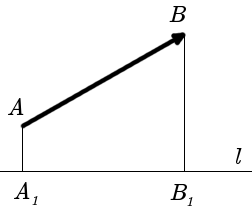 |
| Imagen. 1 |
Definición. La proyección vectorial del vector a sobre el vector b se denomina el vector que es igual a la proyección ortogonal del vector a sobre el eje que atraviesa el vector b.
Definición. La proyección escalar del vector a sobre la dirección del vector b se denomina el número que es igual al valor de la proyección ortogonal del vector a sobre el eje que atraviesa el vector b.
Fórmula del cálculo de la proyección de un vector sobre otro
Para calcular la proyección vectorial del vector a sobre el vector b de la definición del producto escalar sale la fórmula:
| proj ba = | a · b | b |
| |b|2 |
Para calcular la proyección escalar del vector a sobre el vector b de la definición del producto escalarproducto escalar sale la fórmula:
| |proj ba| = | a · b |
| |b| |
Ejemplos de ejercicios sobre el tema de la proyección de vectores
Ejemplos del cálculo de la proyección de un vector para los ejercicios de plano
Ejemplo 1. Calcular la proyección del vector a = {1; 2} sobre el vector b = {3; 4}.
Solución:
Calculemos el producto escalar de estos vectores
a · b = 1 · 3 + 2 · 4 = 3 + 8 = 11Calculemos el módulo del vector b
|b| = √32 + 42 = √9 + 16 = √25 = 5Calculemos la proyección vectorial del vector a sobre el vector b:
| proj ba = | a · b | b = | 11 | {3; 4} ={1.32; 1.76} |
| |b|2 | 25 |
Calculemos la proyección escalar del vector a sobre el vector b:
| |proj ba| = | a · b | = | 11 | = 2.2 |
| |b| | 5 |
Ejemplos del cálculo de la proyección de un vector para los ejercicios de espacio
Ejemplos 2. Calcular la proyección del vector a = {1; 4; 0} sobre el vector b = {4; 2; 4}.
Solución:
Calculemos el producto escalar de estos vectores
a · b = 1 · 4 + 4 · 2 + 0 · 4 = 4 + 8 + 0 = 12Calculemos el módulo del vector b
|b| = √42 + 22 + 42 = √16 + 4 + 16 = √36 = 6Calculemos la proyección vectorial del vector a sobre el vector b:
| proj ba = | a · b | b = | 12 | {4; 2; 4} = { | 4 | ; | 2 | ; | 4 | } |
| |b|2 | 36 | 3 | 3 | 3 |
Calculemos la proyección escalar del vector a sobre el vector b:
| |proj ba| = | a · b | = | 12 | = 2 |
| |b| | 6 |
VectoresCalculación del vector dado en las coordenadas cartesianas de sus puntos inicial y final
Módulo del vector. Longitud del vector
Cosenos directores de un vector
Igualdad de vectores
Vectores ortogonales
Vectores colineales
Vectores coplanares
Ángulo entre vectores
Proyección de un vector
Suma y diferencia de dos vectores
Multiplicación del vector por un número
Producto escalar de vectores
Producto vectorial de vectores
Producto mixtoDescomposición del vector en una base
Dejar comentario
