Vectores colineales. Condiciones de colinearidad de vectores
Definicion. Vectores que son paralelos a una recta o que están en una recta se llaman colineales (fig. 1).
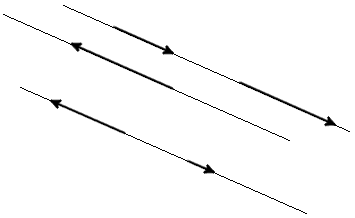 |
| fig. 1 |
Condiciones de colinealidad de vectores
- Dos vectores son colineales si las relaciones de sus coordenadas son iguales.
- Dos vectores son colineales si su producto vectorial equivale a cero.
Así en caso del problema plano los vectores
a =
{ax;
ay} y
b =
{bx;
by} son colineales si:
Ejemplo. Cuál de los vectores
a = {1; 2},
b = {4; 8},
c = {5; 9} son colineales?
Solución:
| Vectores a y b colineales así que |
1 |
= |
2 |
. |
| 4 |
8 |
| Vectores a y с no son colineales así que |
1 |
≠ |
2 |
. |
| 5 |
9 |
| Vectores с y b no son colineales así que |
5 |
≠ |
9 |
. |
| 4 |
8 |
Así en caso del problema espacial los vectores
a =
{ax;
ay;
az} y
b =
{bx;
by;
bz} son colineales si:
Ejemplo. Cuál de los vectores
a = {1; 2; 3},
b = {4; 8; 12},
c = {5; 10; 12} son colineales?
Solución:
| Vectores a y b son colineales así que |
1 |
= |
2 |
= |
3 |
. |
| 4 |
8 |
12 |
| Vectores a y с no son colineales así que |
1 |
= |
2 |
≠ |
3 |
. |
| 5 |
10 |
12 |
| Vectores с y b no son colineales así que |
5 |
= |
10 |
≠ |
12 |
. |
| 4 |
8 |
12 |

