Distancia de un punto a una recta en espacio
Fórmula para hallar la distancia de un punto a la recta en espacio
Si s = {m; n; p} - vector director de la recta l, M1(x1, y1, z1) - punto que está en la recta, entonces ditancia del punto M0(x0, y0, z0) a la recta l se puede calcular, utilizando la fórmula
| d = | |M0M1×s| |
| |s| |
Deducción de la fórmula para hallar la distancia de un punto a la recta en espacio
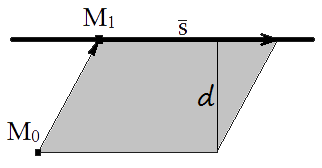
Si hay dada ecuación de la recta l, entonces es fácil calcular s = {m; n; p} - vector director de la recta y M1(x1, y1, z1) - coordenadas del punto que está en está recta. De las propiedades del producto vectorial se sabe que el módulo del producto vectorial equivale a la área del paralelogramo hecho en estos vectores
S = |M0M1×s|.
De otro lado el área del paralelogramo equivale al producto de su lado por la altura trazada hacia este lado
S = |s|d.
En nuestro caso la altura va a equivaler a la distancia del punto hacia plano d, y el lado del paralelogramo equivale al módulo del vector director s.
Al equiparar las áreas no es nada difícil sacar la fórmula de la distancia de un punto a una recta.
Ejemplos de los problemas para hallar la distancia de un punto a la recta en espacio
| x - 3 | = | y - 1 | = | z + 1 |
| 2 | 1 | 2 |
Solución.
De ecuación de la recta sacamos:
s = {2; 1; 2} - vector director de la recta;
M1(3; 1; -1) - el punto que está sobre la recta.
Entonces
M0M1 = {3 - 0; 1 - 2; -1 - 3} = {3; -1; -4}
| M0M1×s = | i | j | k | = |
| 3 | -1 | -4 | ||
| 2 | 1 | 2 |
= i ((-1)·2 - (-4)·1) - j (3·2 - (-4)·2) + k (3·1 -(-1)·2) = {2; -14; 5}
| d = | |M0M1×s| | = | √22 + (-14)2 + 52 | = | √225 | = | 15 | = 5 |
| |s| | √22 + 12 + 22 | √9 | 3 |
Resultado: distancia del punto a la recta equivale a 5.
Dejar comentario
