Ángulo entre dos rectas

y = k₁x + b₁,
y = k₂x + b₂,

entonces se puede encontrar el ángulo entre ellas con ayuda de la fórmula:

Si el denominador es igual a cero (1 + k₁·k₂ = 0), entonces las rectas son perpendiculares.

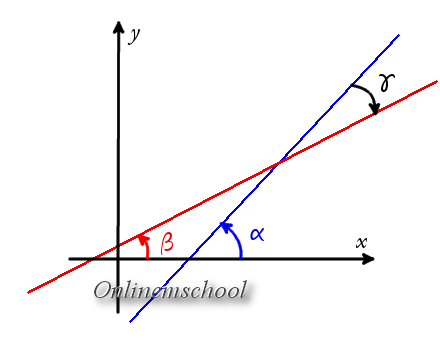
tg α = k₁
tg β = k₂

Por lo tanto es fácil encontrar el ángulo entre dos rectas

γ = α - β

tg γ = tg (α - β) = tg α - tg β1 + tg α ·tg β = k₁ - k₂1 + k₁·k₂

Si la ecuación de la recta se representa paramétricamente

entonces el vector director se ve como {l; m}

Si la ecuación de la recta se representa como

A x + B y + C = 0

entonces para encontrar el vector director se puede utilizar dos puntos en la recta.
Por ejemplo, si C ≠ 0, A ≠ 0, C ≠ 0 , dado que x = 0 => y = -CB entonces el punto en la recta tiene las coordenadas K(0, -CB), dado que y = 0 => x = -CA entonces el punto en la recta tiene las coordenadas M(-CA, 0). Vector director KM = {-CA; CB}.

Si hay dada una ecuación canónica de la recta

x - x₀ l = y - y₀m

entonces el vector director se ve como {l; m}

Si hay dada una ecuación de la recta con la pendiente

y = kx + b

entonces para encontrar el vector director se puede utilizar dos puntos en la recta, por ejemplo, dado que x = 0 => y = b entonces el punto en la recta tiene las coordenadas K(0, b), dado que x = 1 => y = k + b entonces el punto en la recta tiene las coordenadas M(1, k + b). Vector director KM = {1; k}

Si la ecuación de la recta se representa como

A x + B y + C = 0

Entonces el vector normal se ve como {A; B}

Si hay dada una ecuación de la recta con la pendiente

y = kx + b

entonces el vector normal se ve como {1; -k}

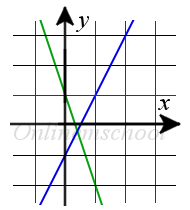
Solución: Utilicemos la fórmula de encontrar el ángulo entre dos rectas con los vectores directores conocidos:

Resultado. γ = 45°

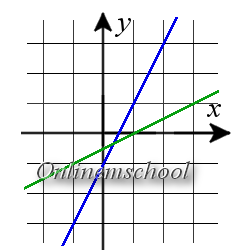
Solución: Utilicemos la fórmula de encontrar el ángulo entre dos rectas con los vectores directores conocidos.

Para la primera recta el vector director {1; 2}, para la segunda recta el vector director {2; 1}

Resultado. φ ≈ 36.87°

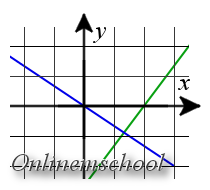
Solución: Para resolver este problema se puede hallar los vectores directores y encontrar el ángulo a partir de los vectores directores o convertir la ecuación en una ecuación con la pendiente y encontrar el ángulo a partir de las pendientes.

Reduzcamos las ecuaciones dadas a las ecuaciones con la pendiente.

2x + 3y = 0 => y = -23x   (k₁ = -23)

x - 23 = y4 => y = 43x - 83   (k₂ = 43)

Resultado. γ ≈ 86.82°

Si hay dada una ecuación canónica de la recta

x - x₀ l = y - y₀m = z - z₀n

entonces el vector director se ve como {l; m; n}

Si la ecuación de la recta se representa paramétricamente

entonces el vector director se ve como {l; m; n}

Solución: Ya que las rectas se representan paramétricamente, entonces {2; 1; -1} es el vector director de la primera recta, {1; -2; 0} es el vector director de la segunda recta.

Resultado. φ = 90°

Solución: Para resolver este ejercicio vamos a encontrar los vectores directores de estas rectas.

La ecuación de la primera recta se representa en la forma canónica, por eso el vector director {3; 4; 5}.

Reduzcamos la segunda ecuación a la forma canónica.

-x - 22 = x - 2-2

1 - 3y = 1 + y-1/3 = y - 1/3-1/3

3z - 52 = z - 5/32/3

Se ha obtenido la ecuación de la segunda recta en la forma canónica

x - 2-2 = y - 1/3-1/3 = z - 5/32/3

{-2; -13; 23} - el vector director de la segunda recta.

Resultado. φ ≈ 74.63°