Triángulo. Fórmulas y propiedades de triángulos
Clasificación de los triángulos
Por la amplitud de sus ángulos
- Triángulo acutángulo – cuando todos sus ángulos internos son agudos.

- Triángulo obtusángulo – si uno de sus ángulos internos es obtuso (mayor de 90°).

- Triángulo rectángulo – si tiene un ángulo interno recto (90°).

Por el número de los lados iguales
- Triángulo escaleno – los tres lados son diferentes.

- Triángulo isósceles – sus dos lados son iguales.

- Triángulo equilátero o triángulo regular – los tres lados son iguales.
Vértices ángulos y lados del triángulo
Propiedades de los angulos y los lados del triángulo
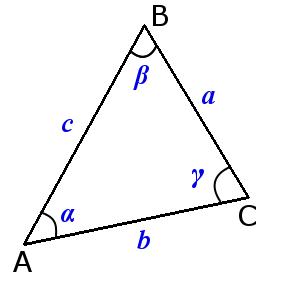
Suma de los ángulos del triángulo es igual a 180°:
α + β + γ = 180°
En un triángulo frente al lado mayor está situado el ángulo mayor, y al revés. Frente a los lados iguales están situados los ángulos iguales:
si α > β, entonce a > b
si α = β, entonce a = b
Suma de las longitudes de dos lados cualquieres de un triángulo es mayor que la longitud del lado restante:
a + b > c
b + c > a
c + a > b
Teorema de los senos.
Los lados de un triángulo son proporcionales a los senos de los ángulos opuestos.
| a | = | b | = | c | = 2R |
| sin α | sin β | sin γ |
Teorema del coseno.
El cuadrado del cualquier lado de un triángulo es igual a la suma de los cuadrados de otros dos lados del triángulo menos el producto doble de estos lados por el coseno del ángulo que ellos forman.
a2 = b2 + c2 - 2bc·cos α
b2 = a2 + c2 - 2ac·cos β
c2 = a2 + b2 - 2ab·cos γ
Ley de proyecciones
Para un triángulo acutángulo:
a = b cos γ + c cos β
b = a cos γ + c cos α
c = a cos β + b cos α
Fórmulas para calcular las longitudes de los lados del triángulo
a =
b =
c =
Medianas del triángulo
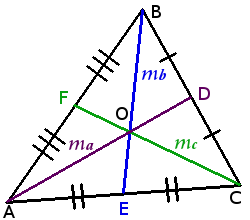
Propiedades de las medianas del triángulo:
- Las medianas de un triángulo concurren en un punto. (El punto de intersección de las medianas se llama centroide)
En el punto de intersección las medianas de un triángulo se dividen a proporción de dos a uno (2:1)
AO OD BO OE CO OF 2 1 Mediana de un triángulo lo divide en dos partes iguales
A∆ABD = A∆ACD
A∆BEA = A∆BEC
A∆CBF = A∆CAF
Las tres medianas dividen al triángulo en 6 triángulos de áreas iguales.
A∆AOF = A∆AOE = A∆BOF = A∆BOD = A∆COD = A∆COE
- De los vectores que forman medianas se puede construir un triángulo.
Fórmulas de las medianas del triángulo
Fórmulas de las medianas del triángulo por medio de los lados
ma =
mb =
mc =
Bisectrices del triángulo
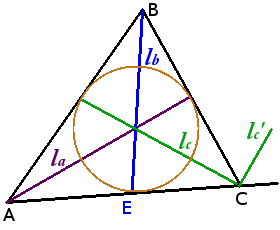
Propiedades de las bisectrices del triángulo:
- Las bisectrices de un triángulo concurren en un punto equidistante de los tres lados del triángulo, - es el centro de la circunferencia inscrita.
Bisectriz de un triángulo divide el lado opuesto en los segmentos proporcionales a los lados adyacentes del triángulo.
AE AB EC BC El ángulo entre las bisectrices del ángulo interior y exterior de un triángulo en el mismo vértice es igual a 90°.
ángulo entre lc y lc' = 90°- Si un triángulo tiene dos bisectrices iguales, entonces el triángulo es isósceles.
Fórmulas de las bisectrices del triángulo
Fórmulas de las bisectrices del triángulo por medio de los lados:
la =
lb =
lc =
donde s =
Fórmulas de las bisectrices de un triángulo por medio de dos lados y un ángulo:
la =
lb =
lc =
Alturas del triángulo
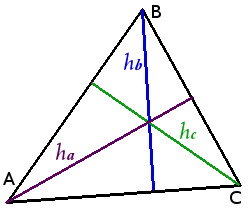
- estar dentro de un triángulo – para un triángulo acutángulo;
- coincidir con su lado – para el cateto de un triángulo rectángulo;
- pasar por fuera de un triángulo – para los ángulos agudos de un triángulo obtusángulo.
Propiedades de las alturas de un triángulo
Fórmulas de las alturas del triángulo
ha = b sin γ = c sin β
hb = c sin α = a sin γ
hc = a sin β = b sin α
ha =
hb =
hc =
ha =
hb =
hc =
Circunferencia inscrita en un triángulo
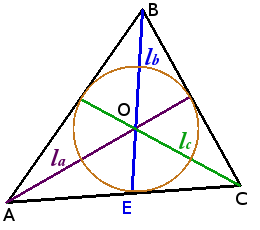
Propiedades de la circunferencia inscrita en un triángulo
Fórmulas del radio de la circunferencia inscrita en un triángulo
r =
r =
Circunferencia circunscrita del triángulo
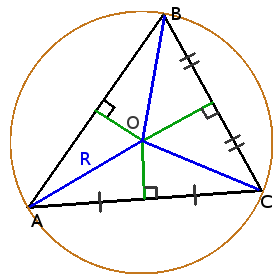
Propiedades de la circunferencia circunscrita de un triángulo
Fórmulas del radio de la circunferencia circunscrita de un triángulo
R =
R =
R =
Conexión entre circunferencia inscrita y circunscrita
d2 = R2 - 2Rr
Paralela media del triángulo
Propiedades de la paralela media del triángulo
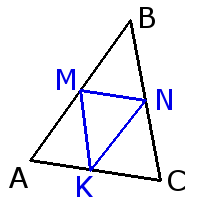
MN =
MN || AC KN || AB KM || BC
A∆MBN =
A∆MAK =
A∆NCK =
∆MBN ∼ ∆ABC
∆AMK ∼ ∆ABC
∆KNC ∼ ∆ABC
∆NKM ∼ ∆ABC
Perímetro del triángulo

Perímetro del triángulo ∆ABC es igual a la suma de longitudes de sus lados.
Fórmulas del área del triángulo

- Fórmulas del área del triángulo por un lado y una altura
Área del triángulo es igual al producto de la longitud de un lado del triángulo por la longitud de la altura trazada a este lado.A =1 2
A =1 2
A =1 2 - Fórmulas del área del triángulo por medio de tres lados
Fórmula de Herón
A = √s(s - a)(s - b)(s - c)donde s =a + b + c 2 - Fórmula del área del triángulo por medio de dos lados y el ángulo entre ellos
Área del triángulo es igual a la mitad del producto de sus dos lados multiplicado por el seno del ángulo entre ellos.A =1 2
A =1 2
A =1 2 - Fórmula del área del triángulo por medio de tres lados y el radio de la circunferencia circunscrita.
A = a · b · с 4R - Fórmula del área del triángulo por medio de tres lados y el radio de la circunferencia inscrita
Área del triángulo es igual al producto del semiperímetro del triángulo por el radio de la circunferencia inscrita.A = s · r
Congruencia de los triángulos
Criterios de congruencia de los triángulos
El primer criterio de la congruencia de los triángulos — por dos lados y el ángulo entre ellos
Si dos lados y el ángulo entre ellos de un triángulo son respectivamente iguales a dos lados y el ángulo entre ellos de otro triángulo, entonces tales triángulos son congruentes.El segundo criterio de la congruencia de los triángulos — por un lado y dos ángulos adyacentes
Si un lado y dos ángulos adyacentes de un triángulo son respectivamente iguales a un lado y dos ángulos adyancentes de otro triángulo, entonces tales triángulos son congruentes.El tercer criterio de la congruencia de los triángulos — por tres lados
Si tres lados de un triángulo son respectivamente iguales a tres lados de otro triángulo, entonces tales triángulos son congruentes.Semejanza de los triángulos
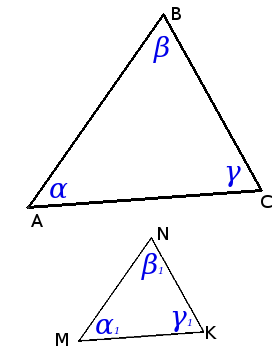
∆АВС ~ ∆MNK => α = α1, β = β1, γ = γ1 и
Criterios de semejanza de los triángulos
El primer criterio de semejanza de los triángulos
Si dos lados de un triángulo son respectivamente iguales a dos lados del otro, entonces tales triángulos son semejantes.El segundo criterio de semejanza de los triángulos
Si los tres lados de un triángulo son proporcionales a los tres lados del otro, entonces tales triángulos son semejantes.El tercer criterio de semejanza de los triángulos
Si dos lados de un triángulo son proporcionales a dos lados del otro, y los ángulos entre estos lados son iguales, entonces tales triángulos son semejantes.Dejar comentario





