Distacia entre dos puntos
Navegación por la página:
Definición. Distancia entre dos puntos es la longitud de un segmento que une estos puntos.
Fórmulas para hallar la distancia entre dos puntos:
- Fórmulas para hallar la distancia entre dos puntos A(xa, ya) y B(xb, yb) en plano:
AB = √(xb - xa)2 + (yb - ya)2 - Fórmulas para hallar la distancia entre dos puntos A(xa, ya, za) y B(xb, yb, zb) en espacio:
AB = √(xb - xa)2 + (yb - ya)2 + (zb - za)2
Deducción de la fórmula para hallar la distancia entre dos puntos en plano
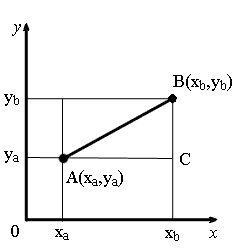
A partir de los puntos A y B vamos a bajar una perpendiculares sobre el eje de coordenadas.
Vamos a ver el triángulo rectángulo ∆ABC. Los catetos de éste son iguales:
BC = yb - ya.
Utilizando el teorema de Pitágoras vamos a hallar la longitud del segmento AB:
Utilizando en esta expresión las longitudes de los segmentos AC y BC, expresados por medio de las coordenadas A y B, obtendremos una fórmula para hallar la distancia entre dos puntos en plano.
Fórmula para hallar la distancia entre dos puntos en plano se deduce analógicamente.
Ejemplos de los problemas para hallar la distancia entre dos puntos
Ejemplo de como hallar la distancia entre dos puntos en plano
Ejemplo 1.
Hallar la distancia entre los puntos A(-1, 3) y B(6,2).
Solución.
Resultado: AB = 5√2.
Ejemplo de como hallar la distancia entre dos puntos en espacio
Ejemplo 2.
Hallar la distancia entre los puntos A(-1, 3, 3) y B(6, 2, -2).
Solución.
= √(6 - (-1))2 + (2 - 3)2 + (-2 - 3)2 = √72 + 12 + 52 = √75 = 5√3
Resultado: AB = 5√3.
Geometría analítica: Introducción e índiceDistacia entre dos puntosPunto medio de un segmento. Coordendas del punto medio de un segmentoEcuación de la rectaPunto de intersección de dos rectasÁngulo entre dos rectasEcuación del planoDistancia de un punto al planoDistancia entre planosDistancia de un punto a una recta en planoDistancia de un punto a una recta en espacioÁngulo entre planosÁngulo entre la recta y el plano
Dejar comentario
