Distancia de un punto al plano
Navegación por la página:
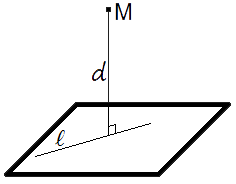
Definición.
Distancia de un punto al plano equivale a la longitud de un perpendicular, bajado de un punto sobre el plano.Fórmula para hallar la distancia de un punto al plano
Si hay dada ecuación del plano Ax + By + Cz + D = 0, entonces la distancia del punto M(Mx, My, Mz) al plano se puede calcular, utilizando la fórmula siguiente:
| d = | |A·Mx + B·My + C·Mz + D| |
| √A2 + B2 + C2 |
Ejemplos de los problemas para hallar la distancia de un punto al plano
Ejemplo 1.
Calcular distancia entre 2x + 4y - 4z - 6 = 0 y punto M(0, 3, 6).
Solución. Ponemos en esta fórmula los coeficientes del plano y coordenadas del punto
| d = | |2·0 + 4·3 + (-4)·6 - 6| | = | |0 + 12 - 24 - 6| | = | |- 18| | = 3 |
| √4 + 16 + 16 | √36 | 6 |
Resultado: distancia del punto al plano es 3.
Geometría analítica: Introducción e índiceDistacia entre dos puntosPunto medio de un segmento. Coordendas del punto medio de un segmentoEcuación de la rectaPunto de intersección de dos rectasÁngulo entre dos rectasEcuación del planoDistancia de un punto al planoDistancia entre planosDistancia de un punto a una recta en planoDistancia de un punto a una recta en espacioÁngulo entre planosÁngulo entre la recta y el plano
Dejar comentario
