Intersección de dos rectas. Punto de intersección de dos rectas
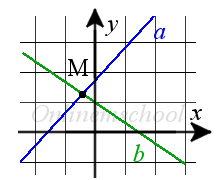
Si el punto M, es el punto de intersección de dos rectas, entonces él debe pertenecer a estas rectas y sus coordenadas deben satisfacer las ecuaciones de estas rectas.
Punto de intersección de dos restas en el plano
- gráfico
- analítico
Si el sistema de ecuaciones:
- tiene la única resolución, entonces las rectas se intersecan;
- tiene un conjunto infinito de resoluciones, entonces las rectas son coincidentes;
- no tiene resolución, entonces las rectas no se intersecan (son paralelas entre si)
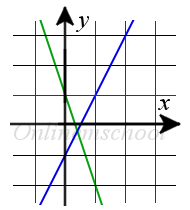
Solución: Para calcular las coordenadas del punto de intersección de dos rectas, resolvamos el sistema de ecuaciones:
De la primera ecuación substraigamos la segunda
De la primera ecuación calculemos el valor de x
Utilicemos el valor de x en la segunda ecuación y calculemos el valor de y
Resultado. El punto de intersección de dos rectas tiene las coordenadas (0.4, -0.2)
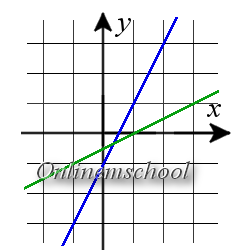
Solución: Para calcular las coordenadas del punto de intersección de dos rectas, resolvamos el sistema de ecuaciones:
Utilicemos el valor de x en la primera ecuación el valor de y de la segunda y tercera ecuación.
Utilicemos el valor de t en la segunda y tercera ecuación
Resultado. El punto de intersección de dos rectas tiene las coordenadas (
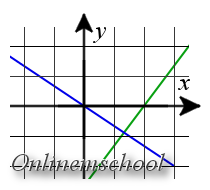
Solución: Para calcular las coordenadas del punto de intersección de dos rectas, resolvamos el sistema de ecuaciones:
De la segunda ecuación expresemos y por x
Utilicemos y en la primera ecuación
Resultado. El punto de intersección de dos rectas tiene las coordenadas (
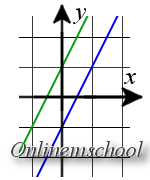
Solución: Las dos rectas están expresadas con las ecuaciones con la pendiente. Ya que k1 = k2 = 2, entonces las rectas son paralelas. Ya que estas rectas no coinciden, entonces no hay puntos de intersección.
Asimismo resolvamos este ejercicio utilizando el sistema de ecuaciones:
De la primera ecuación substraigamos la segunda
En la primera ecuación nos espera una contrariedad (0 ≠ -2), lo que significa que el sistema no tiene resolución – no hay puntos de intersección de dos rectas (las rectas son paralelas).
Resultado. Rectas no se intersecan (las rectas son papalelas).
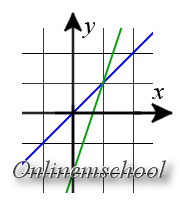
Solución: Utilicemos las coordenadas del punto N en las ecuaciones de las rectas.
1 = 1
1 = 3·1 - 2 = 1
Resultado. Ya que las dos ecuaciones se han convertido en identidades, entonces el punto N es el punto de intersección de estas rectas.
Punto de intersección de dos rectas en el espacio
Si el sistema de ecuaciones:
- tiene la única resolución, entonces las rectas se intersecan;
- tiene un conjunto infinito de resoluciones, entonces las rectas son coincidentes;
- no tiene resolución, entonces las rectas no se intersecan (son paralelas o se cruzan)
Solución: Hagamos un sistema de ecuaciones
Utilicemos el valor de x, y, z de las ecuaciones 1, 2, 3 en las ecuaciones 4, 5, 6
A la sexta ecuación sumemos la quinta ecuación
Utilicemos el valor de b en la cuarta y la quinta ecuación
Resultado. Las rectas se intersecan en el punto con las coordenadas (1, 1, 1).
Solución: Hagamos el sistema de ecuaciones y cambiemos el parámetro t por a en la segunda ecuación
Utilicemos el valor de x, y, z de las ecuaciones 1, 2, 3 en las ecuaciones 4, 5, 6
Utilicemos el valor de t de la sexta ecuación en las demás ecuaciones
Resultado. Ya que -6 ≠
Dejar comentario
