Cuadrado. Fórmulas y propiedades de un cuadrado

Navegación por la página: Definición del cuadrado Las principales propiedades de un cuadrado Diagonal de un cuadrado Perímetro de un caudrado Área de un cuadrado Círculo circunscrito alrededor de un cuadrado Círculo inscrito en un cuadrado

Definición.

Cuadrado es un cuadrilátero cuyos todos los cuatro lados y ángulos son iguales. Los cuadrados se distinguen entre si sólo por la longitud de un lado, pero todos sus cuatro ángulos son rectos, o sea, cada uno mide 90°.


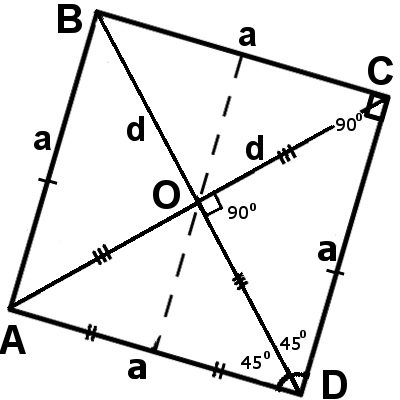
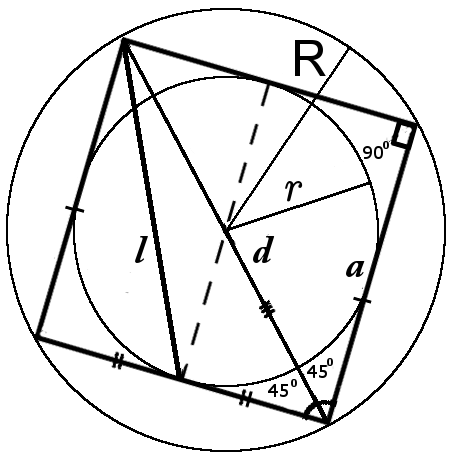
fig.1		fig.2

Las principales propiedades de un cuadrado

Pueden ser un cuadrado el paralelogramo, el rombo o el rectángulo si tienen las mismas longitudes de las diagonales, de los lados y los ángulos iguales.

1. Todos los cuatro lados de un cuadrado tienen la misma longitud, o sea, son iguales:

AB = BC = CD = AD

2. Los lados opuestos de un cuadrado son paralelos:

AB||CD, BC||AD

3. Todos los cuatro ángulos de un cuadrado son rectos:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

4. Suma de los ángulos de un cuadrado es igual a 360:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

5. Las diagonales de un cuadrado tienen la longitud igual:

AC = BD

6. Cada diagonal de un cuadrado lo divide en dos figuras simétricas iguales

7. Las diagonales de un cuadrado se cruzan a un ángulo recto y se dividen una a otra por la mitad:

AC┴BD		AO = BO = CO = DO =	d
			2

8. Punto de intersección de diagonales se llama el centro de un cuadrado y también es el centro de circunferencia inscrita y circunscrita.

9. Cada diagonal divide un ángulo de un cuadrilátero por la mitad, o sea son bisectrizas de los ángulos de un cuadrado:

ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°

10. Las dos diagonales dividen un cuadrado en los cuatro triángulos iguales, siendo de notar que estos triángulos son al mismo tiempo isósceles y rectángulos:

ΔAOB = ΔBOC = ΔCOD = ΔDOA

Diagonal de un cuadrado

Definición.

Se llama diagonal de un cuadrado cualquier segmento que une dos vértices de los ángulos opuestos de un cuadrado.

Diagonal de cualquier cuadrado siempre mide √2 veces más que su lado.

Fórmulas de longitud de diagonal de un cuadrado

1. Fórmula de diagonal de un cuadrado a través de un lado de un cuadrado:

d = a·√2

2. Fórmula de diagonal de un cuadrado a través de la área de un cuadrado:

d = √2A

3. Fórmula de diagonal de un cuadrado a través del perímetro de un cuadrado:

d =	P
	2√2

4. Fórmula de diagonal de un cuadrado a través del radio de una circunferencia circunscritra:

d = 2R

5. Fórmula de diagonal de un cuadrado a través del diámetro de una circunferencia circunscritra:

d = D_о

6. Fórmula de diagonal de un cuadrado a través del radio de una circunferencia inscrita:

d = 2r√2

7. Fórmula de diagonal de un cuadrado a través del diámetro de una circunferencia inscrita:

d = D_в√2

8. Fórmula de diagonal de un cuadrado a través de la longitud del segmento l:

d = l	2√10
	5

Perímetro de un caudrado

Definición.

Se llama perímetro de un caudrado la suma de las longitudes de todos los lados de un cuadrado.

Fórmulas de longitud de perímetro de un cuadrado

1. Fórmula del perímetro de un cuadrado a través del lado de un cuadrado:

P = 4a

2. Fórmula del perímetro de un cuadrado a través la área de un cuadrado:

P = 4√A

3. Fórmula del perímetro de un cuadrado a través del diagonal de un cuadrado:

P = 2d√2

4. Fórmula del perímetro de un cuadrado a través del radio de una circunferencia circunscritra:

P = 4R√2

5. Fórmula del perímetro de un cuadrado a través del diámetro de una circunferencia circunscritra:

P = 2D_о√2

6. Fórmula del perímetro de un cuadrado a través del radio de una circunferencia inscrita:

P = 8r

7. Fórmula del perímetro de un cuadrado a través del diámetro de una circunferencia inscrita:

P = 4D_в

8. Fórmula del perímetro de un cuadrado a través de la longitud del segmento l:

P = l	8
	√5

Área de un cuadrado

Definición.

Se llama área de un cuadrado el espacio limitado por los lados de un cuadrado, o sea, en el marco del perímetro de un cuadrado.

Área de un cuadrado es más grande que un área de cualquier cuadrilátero con un mismo perímetro.

Fórmulas del área de un cuadrado

1. Fórmula del área de un cuadrado a través del lado de un cuadrado:

A = a²

2. Fórmula del área de un cuadrado a través del perímetro de un cuadrado:

A =	P²
	16

3. Fórmula del área de un cuadrado a través del diagonal de un cuadrado:

A =	d²
	2

4. Fórmula del área de un cuadrado a través del radio de una circunferencia circunscritra:

A = 2R²

5. Fórmula del área de un cuadrado a través del diámetro de una circunferencia circunscritra:

A =	D_o²
	2

6. Fórmula del área de un cuadrado a través del radio de una circunferencia inscrita:

A = 4r²

7. Fórmula del área de un cuadrado a través del diámetro de una circunferencia inscrita:

A = D_в²

8. Fórmula del área de un cuadrado a través de la longitud del segmento l:

A = l ²	16
	√5

Círculo circunscrito alrededor de un cuadrado

Definición.

Se llama círculo circunscrito alrededor de un cuadrado un círculo que pasa por cuatro vértices de un cuadrado y tiene su centro en la intersección de las diagonales de un cuadrado.

El radio de una circunferencia circunscrita alrededor de un cuadrado es siempre √2 veces más grande que el radio de una circunferencia inscrita.

El radio de una circunferencia circunscrita alrededor de un cuadrado es igual a la mitad de una diagonal.

El área de un círculo circunscrito alrededor de un cuadrado es π/2 veces más grande que el área de un mismo cuadrado.

Fórmulas de hallar el radio de una circunferencia circunscrita alrededor de un cuadrado

1. Fórmula del radio de una circunferencia circunscrita alrededor de un cuadrado a través del lado de un cuadrado:

R = a	√2
	2

2. Fórmula del radio de una circunferencia circunscrita alrededor de un cuadrado a través del perímetro de un cuadrado:

R =	P
	4√2

3. Fórmula del radio de una circunferencia circunscrita alrededor de un cuadrado a través de la área de un cuadrado:

R =	√2A
	2

4. Fórmula del radio de una circunferencia circunscrita alrededor de un cuadrado a través del diagonal de un cuadrado:

R =	d
	2

5. Fórmula del radio de una circunferencia circunscrita alrededor de un cuadrado a través del diámetro de una circunferencia circunscritra:

R =	D_о
	2

6. Fórmula del radio de una circunferencia circunscrita alrededor de un cuadrado a través del radio de una circunferencia inscrita:

R = r √2

7. Fórmula del radio de una circunferencia circunscrita alrededor de un cuadrado a través del diámetro de una circunferencia inscrita:

R = D_в	√2
	2

8. Fórmula del radio de una circunferencia circunscrita alrededor de un cuadrado a través de la longitud del segmento l:

R = l	√10
	5

Círculo inscrito en un cuadrado

Definición.

Se llama círculo inscrito en un cuadrado un círculo que toca las mitades de los lados de un cuadrado y tiene su centro en la intersección de las diagonales de un cuadrado.

El radio de la circunferencia inscrita es igual a la mitad de un lado de un cuadrado.

El área del círculo inscrito en un cuadrado es 4/π veces menos que el área de un cuadrado.

Fórmulas del radio de un círculo inscrito en un cuadro

1. Fórmula del radio de un círculo inscrito en un cuadrado a través de un lado de un cuadrado:

r =	a
	2

2. Fórmula del radio de un círculo inscrito en un cuadrado a través del diagonal de un cuadrado:

r =	d
	2√2

3. Fórmula del radio de un círculo inscrito en un cuadrado a través del perímetro de un cuadrado:

r =	P
	8

4. Fórmula del radio de un círculo inscrito en un cuadrado a través de la área de un cuadrado:

r =	√A
	2

5. Fórmula del radio de un círculo inscrito en un cuadrado a través del radio de una circunferencia circunscritra:

r =	R
	√2

6. Fórmula del radio de un círculo inscrito en un cuadrado a través del diámetro de una circunferencia circunscritra:

r =	D_о
	2√2

7 Fórmula del radio de un círculo inscrito en un cuadrado a través del diámetro de una circunferencia inscrita:

r =	D_в
	2

8. Fórmula del radio de un círculo inscrito en un cuadrado a través de la longitud del segmento l:

r =	l
	√5

Fórmulas geométricas Triángulo. Fórmulas y propiedades de triángulos Cuadrado. Fórmulas y propiedades de un cuadrado Rectángulo. Fórmulas y propiedades de un rectángulo Paralelogramo. Fórmulas y propiedades de un paralelogramo Rombo. Fórmulas y propiedades de un rombo Trapecio. Fórmulas y propiedades de un trapecio - Trapecio isósceles. Fórmulas y propiedades de un trapecio isósceles - Trapecio rectángulo. Fórmulas y propiedades de un trapecio rectángulo Polígono regular. Fórmulas, características y propiedades del polígono regular Circunferencia, círculo, segmento circular, sector circular. Fórmulas y propiedades Elipse. Fórmulas, atributos y propiedades de la elipse Fórmulas del área de las figuras geométricas Fórmulas del perimetro de las figuras geométricas Fórmulas del volumen de las figuras geométricas Fórmulas de área superficial de figuras geométricas

Todas tablas y fórmulas

Dejar comentario