Rombo. Fórmulas, características y propiedades del rombo

Navegación por la página: Definición del rombo Características del rombo Propiedades básicas del rombo Lado del rombo Diagonales del rombo Perímetro del rombo Área del rombo Circunferencia inscrita en el rombo

Definición.

Rombo es un paralelogramo cuyos lados son iguales. Si todos los ángulos de un rombo son rectos entonces éste se llama el cuadrado.

Los rombos se diferencian entre si por el tamaño de sus lados y por los ángulos que tienen.


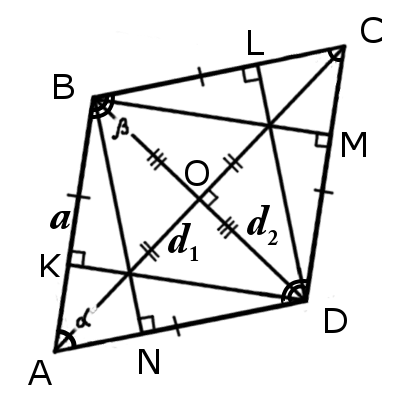
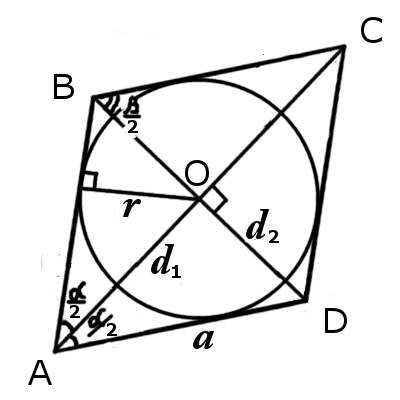
fig.1		fig.2

Características del rombo

Paralelogramo ABCD es un rombo si se cumple al menos una de estas condiciones:

1. Sus dos lados adyacentes son iguales (de esto se deduce que todos los lados son iguales):

АВ = ВС = СD = AD

2. Sus diagonales se cruzan bajo un ángulo recto:

AC┴BD

3. Una de las diagonales (bisectriz) divide los ángulos que la contienen por la mitad:

∠BAC = ∠CAD или ∠BDA = ∠BDC

4. Si todas las alturas son iguales:

BN = DL = BM = DK

5. Si las diagonales dividen un paralelogramo en cuatro triángulos rectángulos iguales:

Δ ABO = Δ BCO = Δ CDO = Δ ADO

6. Si es posible inscribir un círculo en el paralelogramo.

Propiedades del rombo

1. Posee todas las características de un paralelogramo

2. Sus diagonales son perpendiculares:

AC┴BD

3. Las diagonales son bisectrices de sus ángulos:

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

4. Suma de los cuadrados de las diagonales es igual al cuadrado de un lado multiplicado por cuatro:

AC² + BD² = 4AB²

5. Punto de intersección de las diagonales se llama el centro de la simetría de un rombo.

6. En cualquier rombo se puede inscribir una circunferencia.

7. Centro de la circunferencia inscrita en un rombo será el punto de intersección de sus diagonales.

Lado del rombo

Fórmulas para hallar la longitud del lado de un rombo:

1. Fórmula del lado de un rombo a través del área y la altura:

a =	A
	h_a

2. Fórmula del lado de un rombo a través del área y el seno del ángulo:

a =	√A
	√sinα

a =	√A
	√sinβ

3. Fórmula del lado de un rombo a través del área y el radio de la circunferencia inscrita:

a =	A
	2r

4. Fórmula del lado de un rombo a través de dos diagonales:

a =	√d₁² + d₂²
	2

5. Fórmula del lado de un rombo a través de la diagonal y el coseno del ángulo agudo (cos α) o el coseno del ángulo obtuso (cos β):

a =	d₁
	√2 + 2 cosα

a =	d₂
	√2 - 2 cosβ

6. Fórmula del lado de un rombo a través de la diagonal mayor y el ángulo mitad:

a =	d₁
	2cos(α/2)

a =	d₁
	2sin(β/2)

7. Fórmula del lado de un rombo a través de la diagonal menor y el ángulo mitad :

a =	d₂
	2cos(β/2)

a =	d₂
	2sin(α/2)

8. Fórmula del lado de un rombo a través del perímetro:

a =	Р
	4

Diagonales del rombo

Diagonales del rombo.

Se llama la diagonal de un rombo a cualquier segmento que une dos vértices de los ángulos opuestos del rombo.

Rombo tiene dos diagonales – una larga - d₁ y otra corta - d₂

Fórmulas para hallar la longitud del rombo:

1. Fórmulas de la mayor diagonal del rombo a través de un lado y el coseno del ángulo agudo (cosα) o el coseno del ángulo obtuso (cosβ)

d₁ = a√2 + 2 · cosα

d₁ = a√2 - 2 · cosβ

2. Fórmulas de la menor diagonal del rombo a través de un lado y el coseno del ángulo agudo (cosα) o el coseno del ángulo obtuso (cosβ)

d₂ = a√2 + 2 · cosβ

d₂ = a√2 - 2 · cosα

3. Fórmulas de la mayor diagonal del rombo a través de un lado y el ángulo mitad:

d₁ = 2a · cos(α/2)

d₁ = 2a · sin(β/2)

4. Fórmulas de la menor diagonal del rombo a través de un lado y el ángulo mitad:

d₂ = 2a · sin(α/2)

d₂ = 2a · cos(β/2)

5. Fórmulas de las diagonales del rombo a través de un lado y otra diagonal:

d₁ = √4a² - d₂²

d₂ = √4a² - d₁²

6. Fórmulas de las diagonales a través de la tangente del ángulo agudo tgα o él obtuso agudo tgβ y otra diagonal:

d₁ = d₂ · tg(β/2)

d₂ = d₁ · tg(α/2)

7. Fórmulas de las diagonales a través del área y otra diagonal:

d₁ =	2A
	d₂

d₂ =	2A
	d₁

8. Fórmulas de las diagonales a través del seno del ángulo mitad y el radio de la circunferencia inscrita:

d₁ =	2r
	sin(α/2)

d₂ =	2r
	sin(β/2)

Perímetro del rombo

Definición.

Se llama el perímetro del rombo a la suma de las longitudes de todos sus lados.

Se puede hallar la longitud de un lado del rombo a través de las fórmulas mencionadas arriba.

Fórmula para hallar la longitud del perímetro del rombo:

Fórmula del perímetro del rombo a través de un lado del rombo:

P = 4a

Área del rombo

Definición.

Se llama el área del rombo al espacio limitado por los lados del rombo, o sea, en el marco del perímetro del rombo.

Fórmulas para hallar el área del rombo:

1. Fórmula del área del rombo a través de un lado y la altura:

A = a · h_a

2. Fórmula del área del rombo a través de un lado y el seno de cualquier ángulo:

A = a² · sinα

3. Fórmula del área del rombo a través de un lado y el radio:

A = 2a · r

4. Fórmula del área del rombo a través de dos diagonales:

A =	1	d₁d₂
	2

5. Fórmula del área del rombo a través del seno del ángulo y el radio de la circunferencia inscrita:

A =	4r²
	sinα

6. Fórmula del área del rombo a través de la mayor diagonal y la tangente del ángulo agudo (tgα) o la menor diagonal y la tangente del ángulo obtuso (tgβ):

A =	1	d₁² · tg(α/2)
	2

A =	1	d₂² · tg(β/2)
	2

Circunferencia inscrita en el rombo

Definición.

Se llama el círculo inscrito en un rombo al círculo adyacente a todos los lados del rombo y cuyo centro está en la intersección de las diagonales del rombo.

Fórmulas para hallar el radio del círculo inscrito en el rombo:

1. Fórmula del radio del círculo inscrito en el rombo a través de la altura del rombo:

r =	h
	2

2. Fórmula del radio del círculo inscrito en el rombo a través del área y un lado del rombo:

r =	A
	2a

3. Fórmula del radio del círculo inscrito en el rombo a través del área y el seno del ángulo:

r =	√A · sinα
	2

4. Fórmula del radio del círculo inscrito en el rombo a través de un lado y el seno de cualquier ángulo:

r =	a · sinα
	2

r =	a · sinβ
	2

5. Fórmula del radio del círculo inscrito en el rombo a través de la diagonal y el seno del ángulo:

r =	d₁ · sin(α/2)
	2

r =	d₂ · sin(β/2)
	2

6. Fórmula del radio del círculo inscrito en el rombo a través de dos diagonales:

r =	d₁ · d₂
	2√d₁² + d₂²

7. Fórmula del radio del círculo inscrito en el rombo a través de dos diagonales y un lado:

r =	d₁ · d₂
	4a

Fórmulas geométricas Cuadrado. Fórmulas y propiedades de un cuadrado Rectángulo. Fórmulas y propiedades de un rectángulo Paralelogramo. Fórmulas y propiedades de un paralelogramo Rombo. Fórmulas y propiedades de un rombo Trapecio. Fórmulas y propiedades de un trapecio - Trapecio isósceles. Fórmulas y propiedades de un trapecio isósceles - Trapecio rectángulo. Fórmulas y propiedades de un trapecio rectángulo Polígono regular. Fórmulas, características y propiedades del polígono regular Fórmulas del área de las figuras geométricas Fórmulas del perimetro de las figuras geométricas Fórmulas del volumen de las figuras geométricas Fórmulas de área superficial de figuras geométricas

Todas tablas y fórmulas

Dejar comentario