Rectángulo. Fórmulas y propiedades del rectángulo

Navegación por la página: Definición del rectángulo Las principales propiedades del rectángulo Lados del rectángulo Diagonal del rectángulo Perímetro del rectángulo Área del rectángulo Circunferencia circunscrita alrededor del rectángulo Ángulo entre el lado y la diagonal del rectángulo Ángulo entre las diagonales del rectángulo

Definición.

Rectángulo es un cuadrilátero cuyos dos lados opuestos son iguales y todos los cuatro ángulos son iguales también.

Los rectángulos se diferencian entre si solo por la relación del lado largo al corto, pero todos sus cuatro ángulos son rectos, o sea, miden 90° cada uno.

Al lado largo de un rectángulo lo llaman la longitud de un rectángulo y al corto lo llaman la anchura de un rectángulo.

Los lados de un rectángulo son al mismo tiempo sus alturas.


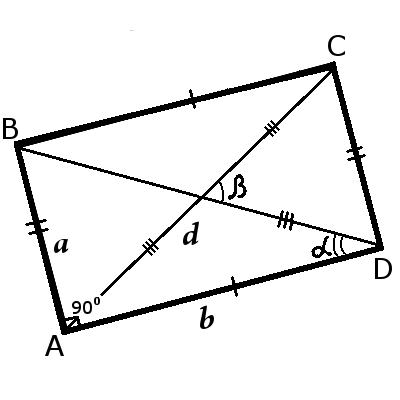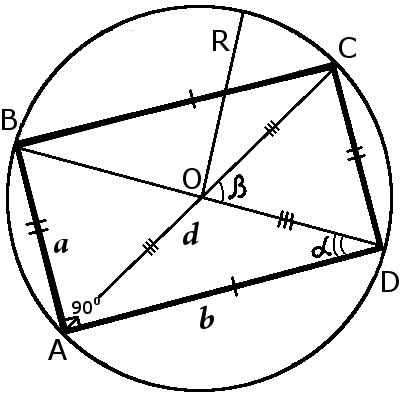fig.1		fig.2

Las principales propiedades del rectángulo

Pueden ser un rectángulo tales figuras como un paralelogramo, un cuadrado o un rombo.

1. Los lados opuestos de un rectángulo tienen la misma longitud, o sea, son iguales:

AB = CD, BC = AD

2. Los lados opuestos de un rectángulo son paralelos:

AB||CD, BC||AD

3. Los lados adyacentes de un rectángulo siempre son perpendiculares:

AB _┴ BC, BC _┴ CD, CD _┴ AD, AD _┴ AB

4. Todos los cuatro ángulos de un rectángulo son rectos:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

5. Suma de los ángulos de un rectángulo es igual a 360°:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

6. Las diagonales de un rectángulo tienen las longitudes iguales:

AC = BD

7. Suma de los cuadrados de las diagonales de un rectángulo es igual a la suma de los cuadrados de los lados:

2d² = 2a² + 2b²

8. Сada diagonal de un rectángulo lo divide en dos figuras iguales, o sea, en dos triángulos rectangulares.

9. Las diagonales de un rectángulo se cruzan y en el punto de la intersección se dividen por la mitad:

		AO = BO = CO = DO =	d
			2

10. El punto de la intersección de las diagonales se llama el centro de un rectángulo y también es el centro de la circunferencia circunscrita

11. La diagonal de un rectángulo es el diámetro de la circunferencia circunscrita

12. Siempre se puede circunscribir una circunferencia alrededor de un rectángulo ya que la suma de los ángulos opuestos es 180°:

∠ABC + ∠CDA = 180° ∠BCD + ∠DAB = 180°

13. En un rectángulo cuya longitud no es igual a la anchura no se puede inscribir una circunferencia ya que las sumas de los lados opuestos no son iguales entre si (se puede inscribir una circunferencia sólo en el caso exclusivo de un rectángulo que es un cuadrado).

Lados del rectángulo

Definición.

Se llama la longitud de un rectángulo a la longitud del par más largo de sus lados. Se llama la anchura de un rectángulo a la longitud del par más corto de sus lados.

Fórmulas para hallar la longitud de los lados de un rectángulo

1. Fórmula del lado de un rectángulo (de longitud y de anchura de un rectángulo) a través de una diagonal y otro lado:

a = √d² - b²

b = √d² - a²

2. Fórmula del lado de un rectángulo (de longitud y de anchura de un rectángulo) a través del área y otro lado:

a =	A
	b

b =	A
	a

3. Fórmula del lado de un rectángulo (de longitud y de anchura de un rectángulo) a través del perímetro y otro lado:

a =	P - 2b
	2

b =	P - 2a
	2

4. Fórmula del lado de un rectángulo (de longitud y de anchura de un rectángulo) a través del diámetro y el ángulo α:

a = d sinα

b = d cosα

5. Fórmula del lado de un rectángulo (de longitud y de anchura de un rectángulo) a través del diámetro y el ángulo β:

a = d sin	β
	2

b = d cos	β
	2

Diagonal del rectángulo

Definición.

Se llama la diagonal de un rectángulo a cualquier segmento que une dos vértices de los ángulos opuestos de un rectángulo.

Fórmulas para hallar la longitud de la diagonal de un rectángulo

1. Fórmula de la diagonal de un rectángulo a través de dos lados de un rectángulo (mediante el teorema de Pitágoras):

d = √a² + b²

2. Fórmula de la diagonal de un rectángulo a través del área y cualquier lado:

d =	√A² + a⁴	=	√A² + b⁴
	a		b

3. Fórmula de la diagonal de un rectángulo a través del perímetro y cualquier lado:

d =	√P² - 4Pa + 8a²	=	√P² - 4Pb + 8b²
	2		2

4. Fórmula de la diagonal de un rectángulo a través del radio de la circunferencia circunscrita:

d = 2R

5. Fórmula de la diagonal de un rectángulo a través del diámento de la circunferencia circunscrita:

d = D_о

6. Fórmula de la diagonal de un rectángulo a través del seno del ángulo adyacente a la diagonal y la longitud del lado opuesto a este ángulo:

d =	a
	sin α

7. Fórmula de la diagonal de un rectángulo a través del coseno del ángulo adyacente a la diagonal y la longitud del lado adyacente a este ángulo:

d =	b
	cos α

8. Fórmula de la diagonal de un rectángulo a través del seno del ángulo agudo entre las diagonales y el área de un rectángulo:

d = √2A : sin β

Perímetro del rectángulo

Definición.

Se llama el perímetro de un rectángulo a la suma de las longitudes de todos los lados de un rectángulo.

Fórmulas para hallar la longitud del perímetro de un rectángulo

1. Fórmula del perímetro de un rectángulo a través de dos lados de un rectángulo:

P = 2a + 2b

P = 2(a + b)

2. Fórmula del perímetro de un rectángulo a través del área y cualquier lado:

P =	2A + 2a²	=	2A + 2b²
	a		b

3. Fórmula del perímetro de un rectángulo a través de una diagonal y cualquier lado:

P = 2(a + √d² - a²) = 2(b + √d² - b²)

4. Fórmula del perímetro de un rectángulo a través del radio de la circunferencia circunscrita y cualquier lado:

P = 2(a + √4R² - a²) = 2(b + √4R² - b²)

5. Fórmula del perímetro de un rectángulo a través del diámetro de la circunferencia circunscrita y cualquier lado:

P = 2(a + √D_o² - a²) = 2(b + √D_o² - b²)

Área del rectángulo

Definición.

Se llama el área de un rectángulo al espacio limitado por los lados de un rectángulo, o sea, dentro de la zona del perímetro de un rectángulo.

Fórmulas para hallar el área de un rectángulo

1. Fórmula del área de un rectángulo a través de dos lados:

A = a · b

2. Fórmula del área de un rectángulo a través del perímetro y cualquier lado:

A =	Pa - 2a²	=	Pb - 2b²
	2		2

3. Fórmula del área de un rectángulo a través de una diagonal y cualquier lado:

A = a√d² - a² = b√d² - b²

4. Fórmula del área de un rectángulo a través de una diagonal y el seno del ángulo águdo entre las diagonales:

A =	d² · sin β
	2

5. Fórmula del área de un rectángulo a través del radio de la circunferencia circunscrita y cualquier lado:

A = a√4R² - a² = b√4R² - b²

6. Fórmula del área de un rectángulo a través del diámetro de la circunferencia circunscrita y cualquier lado:

A = a√D_o² - a² = b√D_o² - b²

Circunferencia circunscrita alrededor del rectángulo

Definición.

Se llama la circunferencia circunscrita alrededor de un rectángulo al círculo que pasa por cuatro vértices de un rectángulo cuyo centro es la intersección de las diagonales del rectángulo.

Fórmulas para hallar el radio de la circunferencia circunscrita alrededor de un rectángulo

1. Fórmula del radio de una circunferencia circunscrita alrededor de un rectángulo a través de dos lados:

R =	√a² + b²
	2

2. Fórmula del radio de una circunferencia circunscrita alrededor de un rectángulo a través del perímetro del cuadrado y cualquier lado:

R =	√P² - 4Pa + 8a²	=	√P² - 4Pb + 8b²
	4		4

3. Fórmula del radio de una circunferencia circunscrita alrededor de un rectángulo a través del área de un rectángulo y la longitud de uno de sus lados:

R =	√A² + a⁴	=	√A² + b⁴
	2a		2b

4. Fórmula del radio de una circunferencia circunscrita alrededor de un rectángulo a través de la diagonal de un rectángulo:

R =	d
	2

5. Fórmula del radio de una circunferencia circunscrita alrededor de un rectángulo a través del diámetro de la circunferencia circunscrita:

R =	D_о
	2

6. Fórmula del radio de una circunferencia circunscrita alrededor de un rectángulo a través del seno del ángulo adyacente a la diagonal y la longitud del lado opuesto a este ángulo:

R =	a
	2sin α

7. Fórmula del radio de una circunferencia circunscrita alrededor de un rectángulo a través del coseno del ángulo adyacente a la diagonal y la longitud del lado adyacente a este ángulo:

R =	b
	2cos α

8. Fórmula del radio de una circunferencia circunscrita alrededor de un rectángulo a través del seno del ángulo agudo entre las diagonales y el área del rectángulo:

R =	√2S : sin β
	2

Ángulo entre el lado y la diagonal del rectángulo

Fórmulas para hallar el ángulo entre el lado y la diagonal

1. Fórmula para hallar el ángulo entre el lado y la diagonal de un rectángulo a través de la diagonal y un lado:

sin α =	a
	d

cos α =	b
	d

2. Fórmula para hallar el ángulo entre el lado y la diagonal de un rectángulo a través del ángulo entre las diagonales:

α =	β
	2

Ángulo entre las diagonales del rectángulo

Fórmulas para hallar el ángulo entre las diagonales de un rectángulo

1. Fórmula para hallar el ángulo entre las diagonales de un rectángulo a través del ángulo entre el lado y la diagonal:

β = 2α

2. Fórmula para hallar el ángulo entre las diagonales de un rectángulo a través del área y la diagonal:

sin β =	2A
	d²

Fórmulas geométricas Triángulo. Fórmulas y propiedades de triángulos Cuadrado. Fórmulas y propiedades de un cuadrado Rectángulo. Fórmulas y propiedades de un rectángulo Paralelogramo. Fórmulas y propiedades de un paralelogramo Rombo. Fórmulas y propiedades de un rombo Trapecio. Fórmulas y propiedades de un trapecio - Trapecio isósceles. Fórmulas y propiedades de un trapecio isósceles - Trapecio rectángulo. Fórmulas y propiedades de un trapecio rectángulo Polígono regular. Fórmulas, características y propiedades del polígono regular Circunferencia, círculo, segmento circular, sector circular. Fórmulas y propiedades Elipse. Fórmulas, atributos y propiedades de la elipse Fórmulas del área de las figuras geométricas Fórmulas del perimetro de las figuras geométricas Fórmulas del volumen de las figuras geométricas Fórmulas de área superficial de figuras geométricas

Todas tablas y fórmulas

Dejar comentario