Resta de números naturales. Resta con llevadas
Operación de restar es inversa a la operación de sumar. Es decir, al par de números naturales a y b les corresponde el número natural c
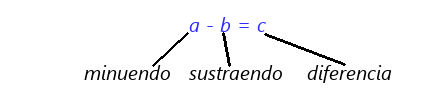 que lleva a que c + b = a.
que lleva a que c + b = a.
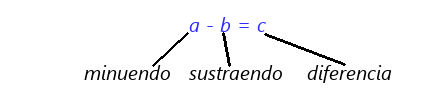 que lleva a que c + b = a.
que lleva a que c + b = a.
El número c se denomina la diferencia de los números a y b; número a - minuendo; número b - sustraendo.
Para los números naturales la diferencia c = a - b existe sólo cuando a > b.
Propiedades de la operación de resta de números:
- a - (b + c) = (a - b) - c = (a - c) - b;
- (a + b) - c = (a - c) + b = a + (b - c);
- a - (b - c) = (a - b) + c
Resta con llevadas
Es cómodo restar con llevadas dos números que constan de dos cifras y más. Para ello escribamos los números uno bajo el otro conforme a los valores posicionales. El proceso de restar se realiza de la derecha a la izquierda: primero se restan las unidades, luego van las decenas, centenas, miles y así por el estilo. La resta de cada columna se escribe por su debajo. Si es necesario se presta 1 de la columna vecina a la izquierda (es decir, del valor posicional superior).
Si el minuendo es menor que el sustraendo a < b, entonces para restar se puede usar la siguiente propiedad:
a - b = -(b - a)
es decir restar minuendo del sustraendo y escribir el resultado con el signo contrario.Ejemplos de resta con llevadas
Ejemplo 1. Resta con llevadas de dos números de tres cifras
| - | 4 | 5 | 6 |
| 2 | 0 | 3 | |
| 2 | 5 | 3 |
6 - 3 = 3
5 - 0 = 5
4 - 2 = 2
Ejemplo 2. Resta con llevadas de dos números de tres cifras
| 1 | |||
| - | 7 | 4 | 3 |
| 6 | 1 | 4 | |
| 1 | 2 | 9 |
ya que 3 < 4, entonces prestamos uno (1) del valor posicional precedente
13 - 4 = 9
4 - 1 - 1 = 2
7 - 6 = 1
Ejemplo 3. Usar resta con llevadas para calcular el valor 450002 - 35005.
| 1 | 1 | 1 | 1 | |||
| - | 4 | 5 | 0 | 0 | 0 | 2 |
| 3 | 5 | 0 | 0 | 5 | ||
| 4 | 1 | 4 | 9 | 9 | 7 |
ya que 2 < 5, entonces prestamos uno (1) у предыдущего разряда
12 - 5 = 7
ya que 0 < 1, entonces prestamos uno (1) del valor posicional precendente
10 - 1 = 9
ya que 0 < 1, entonces prestamos uno (1) del valor posicional precendente
10 - 1 = 9
ya que 0 < 5, entonces prestamos uno (1) del valor posicional precendente
10 - 1 - 5 = 4
5 - 1 - 3 = 1
Números
Números naturales
Adición de números naturales. Suma con llevadas
Resta de números naturales. Resta con llevadas
Dejar comentario
