Cuadrado de una suma

• Cuadrado de una suma - definición
• Deducción de la fórmula de cuadrado de una suma
• Aplicación de la fórmula de cuadrado de una suma
• Interpretación geométrica
• Ejemplos de problemas sobre aplicación de la fórmula de cuadrado de una suma

Cuadrado de una suma de dos términos es igual al cuadrado del primero más el doble del producto del primero y el segundo, más el cuadrado del segundo: (a + b)² = a² + 2ab + b²

Para comprobar la validez de la fórmula del cuadrado de una suma es suficiente multiplicar los términos abriendo los paréntesis:

(a + b)² = (a + b)·(a + b) = a² + ab + ba + b² = a² + 2ab + b²

Es conveniente utilizar la fórmula de cuadrado de una suma para:

• abrir los paréntesis
• para simplificación de las expresiones
• para calcular los cuadrados de unos números grandes sin utilizar calculadora o el multiplicación larga

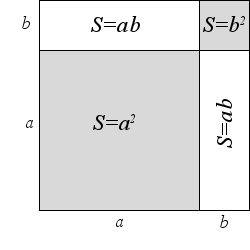
La fórmula de cuadrado de la suma de dos números positivos a y b se puede expresar geométricamente

Vamos a ver un cuadrado con el lado (a + b), su área es (a + b)².

En los ángulos opuestos del cuadrado actual construyamos otros cuadrados con los lados a y b.

Entonces el gran cuadrado inicial será dividido en cuatro partes: dos cuadrados con las áreas a² y b², y también dos rectángulos con las áreas ab. Entonces, como resultado tenemos

(a + b)² = (a + b)·(a + b) = a² + b² + ab+ ab = a² + 2ab + b²

Abrir los paréntesis (x + 3)².

Solución:

(x + 3)² = x² + 2·3·x + 3² = x² + 6x + 9

Abrir los paréntesis (2x + 3y²)².

Solución:

(2x + 3y²)² = (2x)² + 2·(2x)·(3y²) + (3y²)² = 4x² + 12xy² + 9y⁴

Simplificar la expresión 9x² + 6x + 1(3x + 1).

Solución:

Se puede notar que la expresión en el numerador es el cuadrado de una suma descompuesto

9x² + 6x + 1(3x + 1) = (3x + 1)²(3x + 1) = 3x + 1

Calcular 71².

Solución:

71² = (70 + 1)² = 70² + 2·70·1 + 1² = 4900 + 140 + 1 = 5041